题目内容
如图,直线y=- x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).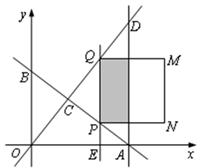
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4,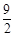 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
(1)(3,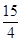 );(2)当0<t≤
);(2)当0<t≤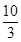 时,S=-2(t-
时,S=-2(t-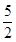 )2+
)2+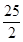 ,当
,当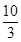 ≤t<5时,S=4(t-5)2,
≤t<5时,S=4(t-5)2,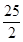 ;(3)
;(3)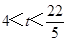 .
.
解析试题分析:(1)利用已知函数解析式,求两直线的交点,得点C的坐标即可;
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况,进而分类讨论得出;
(3)利用(2)中所求,结合二次函数最值求法求出即可.
试题解析:(1)由题意,得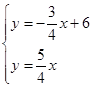 ,解得:
,解得: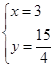 ,
,
∴C(3,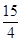 );
);
(2)∵直线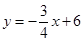 分别与x轴、y轴交于A、B两点,
分别与x轴、y轴交于A、B两点,
∴y=0时,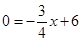 ,解得;x=8,
,解得;x=8,
∴A点坐标为;(8,0),
根据题意,得AE=t,OE=8-t.
∴点Q的纵坐标为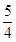 (8-t),点P的纵坐标为-
(8-t),点P的纵坐标为-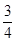 (8-t)+6=
(8-t)+6=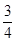 t,
t,
∴PQ=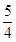 (8-t)-
(8-t)-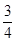 t=10-2t.
t=10-2t.
当MN在AD上时,10-2t=t,
∴t=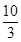 .
.
当0<t≤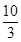 时,S=t(10-2t),即S=-2t2+10t.
时,S=t(10-2t),即S=-2t2+10t.
当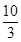 <t<5时,S=(10-2t)2,即S=4t2-40t+100;
<t<5时,S=(10-2t)2,即S=4t2-40t+100;
当0<t≤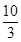 时,S=-2(t-
时,S=-2(t-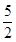 )2+
)2+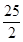 ,
,
∴t=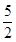 时,S最大值=
时,S最大值=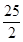 .
.
当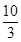 ≤t<5时,S=4(t-5)2,
≤t<5时,S=4(t-5)2,
∵t<5时,S随t的增大而减小,
∴t=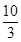 时,S最大值=
时,S最大值=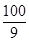 .
.
∵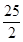 >
>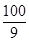 ,
,
∴S的最大值为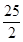 .
.
(3)点(4,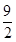 )在正方形PQMN内部时t的取值范围是
)在正方形PQMN内部时t的取值范围是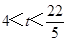 .
.
考点: 一次函数综合题.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时(包括15吨),采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家4、5月份的用水量及收费情况如下表:
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?

 (x>0)的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形 的边
的边 恰好被点
恰好被点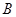 平分,边
平分,边 交双曲线于
交双曲线于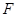 点,四边形
点,四边形 的面积为2.
的面积为2.
 的解集
的解集 与
与 轴相交于点A,与
轴相交于点A,与 轴相交于点B.
轴相交于点B.
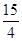 ,试求点P的坐标.
,试求点P的坐标.