题目内容
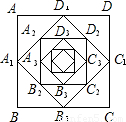
 如图,顺次连接边长为1的正方形ABCD各边中点得正方形A1B1C1D1,顺次连接正方形A1B1C1D1的中点得正方形A2B2C2D2,以此下去则正方形A4B4C4D4 的面积为________.
如图,顺次连接边长为1的正方形ABCD各边中点得正方形A1B1C1D1,顺次连接正方形A1B1C1D1的中点得正方形A2B2C2D2,以此下去则正方形A4B4C4D4 的面积为________.
2-4(或 )
)
分析:根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,以此类推可得正方形A4B4C4D4 的面积.
解答:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即 ;
;
顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即 ;
;
顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半,即 .
.
故答案为: 或2-4.
或2-4.
点评:本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.
 )
)分析:根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,以此类推可得正方形A4B4C4D4 的面积.
解答:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即
 ;
;顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即
 ;
;顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即

顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半,即
 .
.故答案为:
 或2-4.
或2-4.点评:本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.

练习册系列答案
相关题目
 如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=6,DF=4,则菱形ABCD的边长为( )
如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=6,DF=4,则菱形ABCD的边长为( )A、4
| ||
B、3
| ||
| C、5 | ||
| D、7 |
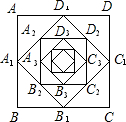 如图,顺次连接边长为1的正方形ABCD各边中点得正方形A1B1C1D1,顺次连接正方形A1B1C1D1的中点得正方形A2B2C2D2,以此下去则正方形A4B4C4D4 的面积为
如图,顺次连接边长为1的正方形ABCD各边中点得正方形A1B1C1D1,顺次连接正方形A1B1C1D1的中点得正方形A2B2C2D2,以此下去则正方形A4B4C4D4 的面积为 (2012•永嘉县一模)如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=4,DF=3,则菱形ABCD的边长为( )
(2012•永嘉县一模)如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=4,DF=3,则菱形ABCD的边长为( )