题目内容
已知⊙O的半径为4,半径OC所在的直线垂直弦AB,P为垂足,AB= ,则S△ABO:S△ABC=________.
,则S△ABO:S△ABC=________.
7:1或7:15
分析:根据题意画出图形,先根据垂径定理得出AP的长,再由勾股定理得出OP的长,利用三角形的面积公式求解.
解答: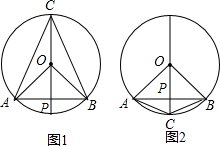 解:∵OC⊥AB,AB=
解:∵OC⊥AB,AB= ,
,
∴AP= AB=
AB= ,
,
在Rt△AOP中,
∵OA=4,AP= ,
,
∴OP= =
=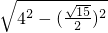 =
= ,
,
∴S△ABO= AB•OP=
AB•OP= ×
× ×
× =
=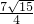 ,
,
如图1所示:
∵OP= ,
,
∴PC=OP+OC= +4=
+4= ,
,
∴S△ABC= AB•PC=
AB•PC= ×
× ×
× =
=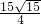 ,
,
∴S△ABO:S△ABC=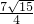 :
: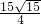 =7:15;
=7:15;
如图2所示:
∵OP= ,OC=4,
,OC=4,
∴PC=OC-OP=4- =
= ,
,
∴S△ABC= AB•PC=
AB•PC= ×
× ×
× =
= ,
,
∴S△ABO:S△ABC=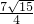 :
: =7:1.
=7:1.
故答案为:7:1或7:15.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:根据题意画出图形,先根据垂径定理得出AP的长,再由勾股定理得出OP的长,利用三角形的面积公式求解.
解答:
 解:∵OC⊥AB,AB=
解:∵OC⊥AB,AB= ,
,∴AP=
 AB=
AB= ,
,在Rt△AOP中,
∵OA=4,AP=
 ,
,∴OP=
 =
=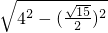 =
= ,
,∴S△ABO=
 AB•OP=
AB•OP= ×
× ×
× =
=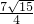 ,
,如图1所示:
∵OP=
 ,
,∴PC=OP+OC=
 +4=
+4= ,
,∴S△ABC=
 AB•PC=
AB•PC= ×
× ×
× =
=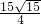 ,
,∴S△ABO:S△ABC=
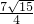 :
: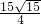 =7:15;
=7:15;如图2所示:
∵OP=
 ,OC=4,
,OC=4,∴PC=OC-OP=4-
 =
= ,
,∴S△ABC=
 AB•PC=
AB•PC= ×
× ×
× =
= ,
,∴S△ABO:S△ABC=
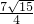 :
: =7:1.
=7:1.故答案为:7:1或7:15.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
| A、在圆上 | B、在圆外 | C、在圆内 | D、不确定 |

 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2