题目内容
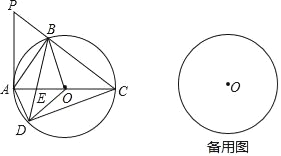
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.
【答案】(1)证明见解析;(2)S△ABC=![]() 或
或![]() ;(3)b2=ac.
;(3)b2=ac.
【解析】试题分析:(1)欲证明PA是切线,只要证明PA⊥OA即可;
(2)分两种情形分别求解即可;
(3)只要证明AD∥OB,可得△AED∽△OEB,推出 ,再推出
,再推出![]() 可得
可得![]() =(
=(![]() )2,b2=ac.
)2,b2=ac.
试题解析:
(1)证明:∵BD=BC,
∴∠BDC=∠BCD,
∵∠P=∠BCD,∠BAC=∠BDC,
∴∠P=∠BAC,
∵AC是直径,
∴∠ABC=∠ABP=90°,
∴∠P+∠BAP=90°,
∴∠BAP+∠BAC=90°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)解:①当∠OED=90°时,CB=CD=BD,△ABC是等边三角形,可得∠ACB=30°,
∵AC=2,
∴AB=1,BC=![]() ,
,
∴S△ABC=![]() .
.
②当∠DOE=90°时,易知∠AOB=45°,△ABC的AC边上的高=![]() ,
,
∴S△ABC=![]() .
.
(3)∵BD=BC,OD=OC,BO=BO,
∴△BOD≌△BOC,
∴∠OBD=∠OBC,
∵OB=OD=CO,
∴∠OBD=∠OBC=∠ODB=∠OCB,
∵∠ADB=∠OCB,
∴∠ADB=∠OBD,
∴AD∥OB,
∴△AED∽△OEB,
∴ ,
,
∵![]() ,
,
∴![]() =(
=(![]() )2,
)2,
∴b2=ac.


【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.

(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| 进价 | 售价 |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
![]() 如何进货,进货款恰好为46000元?
如何进货,进货款恰好为46000元?
![]() 为确保乙型节能灯顺利畅销,在
为确保乙型节能灯顺利畅销,在![]() 的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为
的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为![]() ,请问乙型节能灯需打几折?
,请问乙型节能灯需打几折?



