题目内容
20. 在△ABC中,AB=AC,点O和I分别为△ABC的外心和内心,点D在边AC上,OD⊥CI,求证:ID∥AB.
在△ABC中,AB=AC,点O和I分别为△ABC的外心和内心,点D在边AC上,OD⊥CI,求证:ID∥AB.
分析 首先证明B、I、O、D四点共圆,再证明∠2=∠CAB,于是根据平行线的判定定理得到ID∥AC.
解答 证明:(1)延长AO交BC于M,连接OC.
∵AB=AC,O为外心,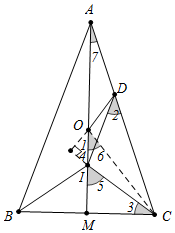
∴AM⊥BC,
∴AM平分∠BAC,
∴∠CAB=2∠7,
∵I为内心,
∴点I在AM上,CI平分∠BCA,
∴∠3=∠ACI,
∵CI⊥DO,
∴∠1+∠4=90°,
∵∠3+∠5=90°,∠4=∠5,
∴∠1=∠3,
∴∠1=∠ACI,
而∠1+∠DOI=180°,
∴∠ACI+∠DOI=180°,
∴C、I、O、D四点共圆;
∴∠2=∠6,
∵点O为外心,
∴OC=OA,
∴∠7=∠OCA,
∴∠6=2∠7=∠2
而∠CAB=2∠7,
∴∠2=∠CAB,
∴ID∥AB.
点评 本题考查了圆的综合题:熟练掌握三角形内心与外心的性质、圆周角定理、四点共圆的判定方法和等腰三角形的性质;会运用平行线的判定定理证明两直线平行.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
12.把(-5)+(-3)+(+1)+(-16)写成省略括号和加号的形式是( )
| A. | -5+3+1-16 | B. | -5-3+1-16 | C. | -5-3-1+16 | D. | -5+3+1+16 |
9.向东行进-50m表示的意义是( )
| A. | 向东行进50 m | B. | 向南行进50 m | C. | 向北行进50 m | D. | 向西行进50 m |
10.李强靠勤工俭学的收入维持上大学的费用.表是他某一周的收支情况表(收入为正,支出为负,单位为元)
(1)到本周末,李强有多少节余?
(2)照这样,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
| 周一 | 周二 | 三 | 四 | 五 | 六 | 日 |
| +12 | +14 | 0 | +25 | +16 | +13 | +11 |
| -8 | -12 | -19 | -10 | -9 | -11 | -8 |
(2)照这样,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
 如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.
如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.