题目内容

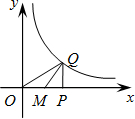
如图，点P是x轴上的一个动点，过点P作x轴的垂线QP交双曲线 $数学公式$ 于点Q，连接OQ，QM是Rt△QOP的OP边上的中线，则当点P沿x轴的正方向运动时，Rt△QPM的面积

A.
逐渐增大
B.
逐渐减小
C.
保持不变
D.
无法确定

C
分析：先根据反比例函数系数k的几何意义求出△OPQ的值，再根据中点的性质即可得出结论．
解答：∵点P是x轴上的一个动点，Q是双曲线 $\text{[math]}$ 的点，QP⊥x轴，
∴S_△OPQ= $\text{[math]}$ 是定值，
∵点M是OP的中点，
∴S_Rt△QPM= $\text{[math]}$ S_△OPQ是定值．
故选C．
点评：本题考查的是反比例函数系数k的几何意义，在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是 $\text{[math]}$ ，且保持不变．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

如图，点P是x轴上的一点，以P为圆心的圆交x轴于点A（6，0），且与y轴相切于点O，点C（8，0）为x轴上的一点，过点C作⊙P的切线，切点为B．求过B、C两点的直线的解析式．

如图①，已知抛物线y=ax²+bx+c（a≠0）的顶点坐标为M（2，-3），且经过点A（0，1），直线y=x+1与抛物线交于A点和B点．
（1）求这条抛物线的解析式；
（2）求△ABM的面积；
（3）如图②，点P是x轴上的一动点，请探索：
①过点P作PQ∥AB，交BM于点Q，连接AQ，AP，当△APQ的面积最大时，求P的坐标．
②是否存在点P，使得△PAB是直角三角形？若存在，求出所有的点P坐标；若不存在，请说明理由．

如图，点P是x轴上的一个动点，过点P作x轴的垂线QP交双曲线y=

于点Q，连接OQ，QM是Rt△QOP的OP边上的中线，则当点P沿x轴的正方向运动时，Rt△QPM的面积（　　）

A．逐渐增大

B．逐渐减小

C．保持不变

D．无法确定

如图，点P是x轴上的一点，以P为圆心的圆交x轴于点A（6，0），且与y轴相切于点O，点C（8，0）为x轴上的一点，过点C作⊙P的切线，切点为B．求过B、C两点的直线的解析式．

（2005•济宁）如图，点P是x轴上的一点，以P为圆心的圆交x轴于点A（6，0），且与y轴相切于点O，点C（8，0）为x轴上的一点，过点C作⊙P的切线，切点为B．求过B、C两点的直线的解析式．