题目内容
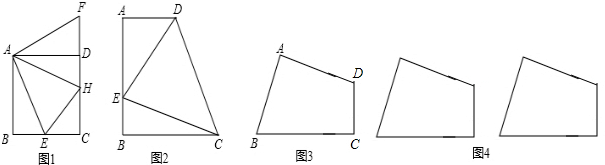
如图①,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF= AB,
AB,
(1)求证:△ABE≌△ADF.
(2)阅读下列材料:如图②,把△ABC沿直线平移线段BC的长度,可以变到△ECD的位置;如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.

图① 图② 图③ 图④
请回答下列问题:
(1)在图①中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
(2)指出图①中线段BE与DF之间的关系.
【答案】
(1)见解析;(2)BE⊥DF,BE=DF
【解析】
试题分析:(1)由ABCD为正方形可得AB=AD,∠DAB=∠DAF=90°,再结合E是AD的中点,AF= AB,即可根据ASA证得两三角形全等;
AB,即可根据ASA证得两三角形全等;
(2)①根据翻转的定义结合图形即可得出答案;②由(1)中的结论可得出BE与DF之间的关系.
(1)∵ABCD为正方形
∴AB=AD,∠DAB=∠DAF=90°
又∵AF= AB,AE=
AB,AE= AD
AD
∴AF=AE
∴△ADF≌△ABE
(2)①由图形可得:△ABE经过旋转可变到△ADF的位置.
②由(1)得:BE⊥DF,BE=DF.
考点:本题考查的是中心对称,全等三角形的判定和性质
点评:解答本题的关键是利用全等三角形的性质与判定结合正方形的性质来解题.

练习册系列答案
相关题目

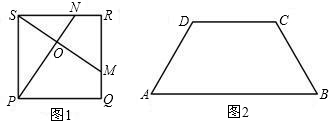 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.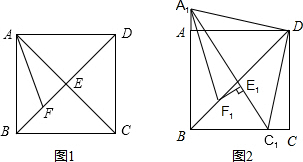 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.