Question

18、如图，在六边形的顶点处，分别标上数3，4，5，6，7，8，能否使任意三个相邻顶点处的三个数之和
（1）大于15？
（2）大于16？若能，请在图中标出来，若不能，请说明理由．

Answer 1

分析：（1）可以分别设这六个数为a，b，c，d，e，f然后将其三个数相加，根据题中给出的条件可知，这把各数的和判断即可得出结论．
（2）根据上题的出的结论直接判断即可解答．

解答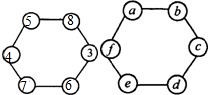：解：（1）能，如图．6个点的顺序分别为8-3-6-7-4-5．任意三个相邻顶点处的和分别为17-16-17-16-17-16．满足均大于15，

（2）但不满足均大于16．
如图，设按要求所填的六个数顺次为a、b、c、d、e、f．它们任意相邻三数和大于16，
即大于或等于17．所以a+b+f≥17，b+c+d≥17，c+d+e≥17，d+e+f≥17，e+f+a≥17，f+a+b≥17．
则每个不等式左边相加一定大于或等于102，即3（a+b+c+d+e+f）≥102
故（a+b+c+d+e+f）≥34．而1+2+3+4+5+6=33，所以不能使每三个相邻的数之和都大于16．

点评：此题主要考查了整数问题的综合应用，分别得出相邻数据之和规律是解题关键．