题目内容
已知:如图①,正方形ABCD中,E为对角线BD上一点,
过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
【小题1】(1)求证:EG=CG;
【小题2】(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【小题3】(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
【小题1】(1)证明:如图①,在Rt△FCD中,
∵ G为DF的中点,
∴CG= FD.…………………………………………..1分
FD.…………………………………………..1分
同理,在Rt△DEF中,EG= FD.
FD.
∴ CG=EG.…………………………………………….2分
【小题2】(2)(1)中结论仍然成立,即EG=CG.…………….3分
证法一:如图②(一),连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点. 在△DAG与△DCG中,
在△DAG与△DCG中,
∵AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG.
∴ AG=CG.…………………………………………………..4分
在△DMG与△FNG中,
∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG. ∴ MG=NG ………………………………………………5分
∴ MG=NG ………………………………………………5分
在矩形AENM中,AM=EN.
在Rt△AMG与Rt△ENG中,
∵AM=EN, MG=NG,
∴ △AMG≌△ENG.
∴ AG=EG.
∴EG=CG. …………………………………………………… 6分
证法二:如图②(二),延长CG至M,使MG=CG,
连接MF,ME,EC,
在△DCG 与△FMG中,
∵ FG=DG,∠MGF=∠CGD,MG=CG,
∴ △DCG ≌△FMG.
∴ MF=CD,∠FMG=∠DCG. ………………………………..4分
∴ MF∥CD∥AB.
∴  .
.
在Rt△MFE与Rt△CBE中,……………………………………….5分
∵MF=CB,EF=BE,
∴ △MFE≌△CBE..
∴  .
. ∴ ∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.
∴ ∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.
∴ △MEC为直角三角形.
∵ MG = CG,∴ EG= MC.
MC.
∴  .……………………………………………6分
.……………………………………………6分
【小题3】(3)如图③,(1)中的结论仍然成立,即EG=CG.
其他的结论还有:EG⊥CG. ………………………..7分
解析

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.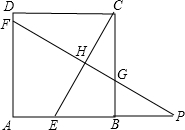 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点.
24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点. 已知:如图,在正方形ABCD中,P为对角线AC上的一动点,PE⊥AB于E,PF⊥BC于F,过点P作DP的垂线交BC于点G,DG交AC于点Q.下列说法:①EF=DP;②EF⊥DP;③
已知:如图,在正方形ABCD中,P为对角线AC上的一动点,PE⊥AB于E,PF⊥BC于F,过点P作DP的垂线交BC于点G,DG交AC于点Q.下列说法:①EF=DP;②EF⊥DP;③ F,BF与边CD交于点G,连接EG.设CE=x.
F,BF与边CD交于点G,连接EG.设CE=x.