题目内容
（1）计算：(2-| 3 |
| 3 |
| 2 |
（2）解方程：
| 6 |
| 2x-4 |
| x+1 |
| x-2 |
| 1 |
| 2 |
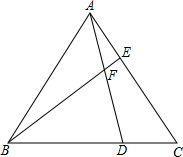
（3）如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．
①求证：△ABE≌△CAD；
②求∠BFD的度数．
分析：（1）根据同底数幂的乘法把（2+
）2012化为（2+
）2011×（2+
），再根据积的乘方可以计算出（2-
）2011×（2+
）2011=1，再代入特殊角的三角函数值，进行计算，注意计算顺序：先算乘法，后算加减；
（2）首先方程两边同时乘以最简公分母2（x-2），再去括号、移项、合并同类项、把x的系数化为1，注意不要忘记检验；
（3）①根据等边三角形的性质可知∠BAC=∠C=60°，AB=CA，结合AE=CD，可证明△ABE≌△CAD；
②根据∠BFD=∠ABE+∠BAD，∠ABE=∠CAD，可知∠BFD=∠CAD+∠BAD=∠BAC=60°．
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
（2）首先方程两边同时乘以最简公分母2（x-2），再去括号、移项、合并同类项、把x的系数化为1，注意不要忘记检验；
（3）①根据等边三角形的性质可知∠BAC=∠C=60°，AB=CA，结合AE=CD，可证明△ABE≌△CAD；
②根据∠BFD=∠ABE+∠BAD，∠ABE=∠CAD，可知∠BFD=∠CAD+∠BAD=∠BAC=60°．
解答：解：（1）原式=（2-
）2011×（2+
）2011×（2+
）-2×
-1
=1×（2+
）-
-1
=1；
（2）去分母得：6-2（x+2）=x-2，
去括号得：6-2x-4=x-2，
移项得：-2x-x=-2+4-6，
合并同类项得：-3x=-4，
把x的系数化为1得：x=
，
检验：把x=
代入最简公分母2（x-2）≠0，
故原分式方程的解为：x=
；
（3）①证明：∵△ABC为等边三角形，
∴∠BAC=∠C=60°，AB=CA．
在△ABE和△CAD中，
∵
，
∴△ABE≌△CAD（SAS），
②解：∵△ABE≌△CAD，
∴∠ABE=∠CAD．
∵∠BFD=∠ABE+∠BAD，
∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
| 3 |
| 3 |
| 3 |
| ||
| 2 |
=1×（2+
| 3 |
| 3 |
=1；
（2）去分母得：6-2（x+2）=x-2，
去括号得：6-2x-4=x-2，
移项得：-2x-x=-2+4-6，
合并同类项得：-3x=-4，
把x的系数化为1得：x=
| 4 |
| 3 |
检验：把x=
| 4 |
| 3 |
故原分式方程的解为：x=
| 4 |
| 3 |
（3）①证明：∵△ABC为等边三角形，∴∠BAC=∠C=60°，AB=CA．
在△ABE和△CAD中，
∵
|
∴△ABE≌△CAD（SAS），
②解：∵△ABE≌△CAD，
∴∠ABE=∠CAD．
∵∠BFD=∠ABE+∠BAD，
∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
点评：此题主要考查了解分式方程，特殊角的三角函数值，零指数幂，幂的乘方，积的乘方，全等三角形的判定与性质，以及三角形的外角内角的关系，关键是同学们要牢固掌握课本知识，熟记课本公式与定理．
练习册系列答案
相关题目
