Question

【题目】如图1，将△ABC纸片沿DE折叠，使点C落在四边形ABDE内点C’的位置，

（1）①若，则 ；

②若，则 ；

③探索 、与之间的数量关系，并说明理由；

（2）直接按照所得结论，填空：

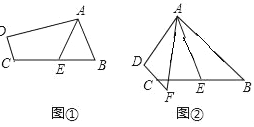
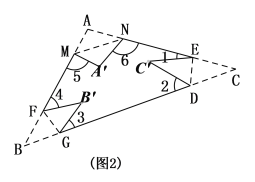
①如图中，将△ABC纸片再沿FG、MN折叠，使点A、B分别落在△ABC内点A’、B’的位置，则 ；

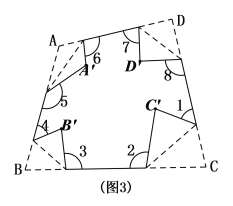
②如图中，将四边形ABCD按照上面方式折叠，则 ；

③若将n边形也按照上面方式折叠，则 ；

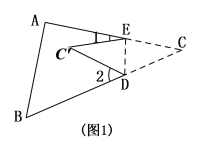
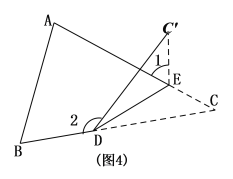
（3）如图，将△ABC纸片沿DE折叠，使点落在△ABC边上方点的位置， 探索、与之间的数量关系，并说明理由.

Answer 1

【答案】（1）①；②；③；（2）①；②；③；（3）

【解析】

（1）①由邻补角的定义可知∠CEC′=160°，∠CDC′=130°，根据折叠的性质可求出∠CED=80°，∠CDE=65°,然后根据三角形内角和定理求解即可；

②由三角形内角和可求出∠CED+∠CDE=138°,再由折叠的性质可知∠CEC′+∠CDC′=276°，然后根据邻补角的定义可求出84°；

③由邻补角定义可知，从而，所以，∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °，结合，可求出；

（2）① 由（1）得2∠C，2∠B，2∠A，从而2(∠A+∠B +∠C)，结合三角形内角和求解即可；

②由①可知， 2(∠A+∠B +∠C+∠D)，结合四边形内角和求解即可;

③由①可知， ；

（3）由外角的性质可知∠2=∠3+∠C，∠3=∠1+∠C，整理可得.

解：（1）①∵，

∴∠CEC′=160°，∠CDC′=130°，

∵ ∠CED=80°，∠CDE=65°,

∴∠C= 180°-80°-65°=35°；

②∵，

∴ ∠CED+∠CDE=180°-42°=138°,

∴∠CEC′+∠CDC′=276°，

∴360°-276°=84°；

③，

因为，，

所以，

因为在四边形中，，

所以，

因为，

所以.

（2）① 由①得

2∠C，2∠B，2∠A，

∴2(∠A+∠B +∠C)=360°;

②∵2∠C，2∠B，2∠A，2∠D，

∴ 2(∠A+∠B +∠C+∠D)=2×360°=720°;

③∵n边形内角和是，

∴ ；

（3）.

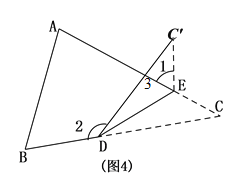
∵∠2=∠3+∠C，

∠3=∠1+∠=∠1+∠C，

∴∠2=∠1+∠C +∠C=∠1+2∠C，

∴.