Question

【题目】小方与同学一起去郊游，看到一棵大树斜靠在一小土坡上，他想知道树有多长，于是他借来测角仪和卷尺．如图，他在点C处测得树AB顶端A的仰角为30°，沿着CB方向向大树行进10米到达点D，测得树AB顶端A的仰角为45°，又测得树AB倾斜角∠1=75°．

（1）求AD的长．
（2）求树长AB．

Answer 1

【答案】
（1）

解：过点A作AE⊥CB于点E，设AE=x，

在Rt△ACE中，∠C=30°，

∴CE= x，

在Rt△ADE中，∠ADE=45°，

∴DE=AE=x，

∴CE﹣DE=10，即 x﹣x=10，

解得：x=5（ +1），

∴AD= x=5 +5

答：AD的长为（5 +5 ）米

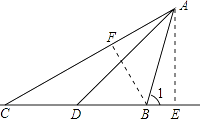
（2）

解：由（1）可得AC=2AE=（10 +10）米，

过点B作BF⊥AC于点F，

∵∠1=75°，∠C=30°，

∴∠CAB=45°，

设BF=y，

在Rt△CBF中，CF= BF= y，

在Rt△BFA中，AF=BF=y，

∴ y+y=（10 +10），

解得：y=10，

在Rt△ABF中，AB= =10 米．

答：树高AB的长度为10 米．

【解析】（1）过点A作AE⊥CB于点E，设AE=x，分别表示出CE、DE，再由CD=10，可得方程，解出x的值，在Rt△ADE中可求出AD；（2）过点B作BF⊥AC于点F，设BF=y，分别表示出CF、AF，解出y的值后，在Rt△ABF中可求出AB的长度．
【考点精析】利用关于仰角俯角问题对题目进行判断即可得到答案，需要熟知仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．