ЬтФПФкШн
ЁОЬтФПЁПЃЈ12ЗжЃЉдФЖСРэНтЃК
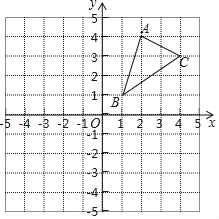
ШчЭМЂйЃЌШчЙћЫФБпаЮABCDТњзуAB=ADЃЌCB=CDЃЌЁЯB=ЁЯD=90ЁуЃЌФЧУДЮвУЧАбетбљЕФЫФБпаЮНазіЁАЭъУРѓнаЮЁБЃЎ
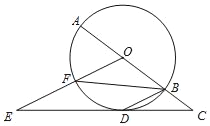
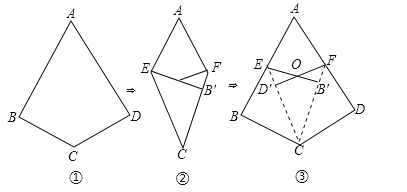
НЋвЛеХШчЭМЂйЫљЪОЕФЁАЭъУРѓнаЮЁБжНЦЌABCDЯШелЕўГЩШчЭМЂкЫљЪОаЮзДЃЌдйеЙПЊЕУЕНЭМЂлЃЌЦфжаCEЃЌCFЮЊелКлЃЌЁЯBCE=ЁЯECF=ЁЯFCDЃЌЕуBЁфЮЊЕуBЕФЖдгІЕуЃЌЕуDЁфЮЊЕуDЕФЖдгІЕуЃЌСЌНгEBЁфЃЌFDЁфЯрНЛгкЕуOЃЎ
МђЕЅгІгУЃК
ЃЈ1ЃЉдкЦНааЫФБпаЮЁЂОиаЮЁЂСтаЮЁЂе§ЗНаЮЫФжжЭМаЮжаЃЌвЛЖЈЮЊЁАЭъУРѓнаЮЁБЕФЪЧ ЃЛ
ЃЈ2ЃЉЕБЭМЂлжаЕФЁЯBCD=120ЁуЪБЃЌЁЯAEBЁф= ЁуЃЛ
ЃЈ3ЃЉЕБЭМЂкжаЕФЫФБпаЮAECFЮЊСтаЮЪБЃЌЖдгІЭМЂлжаЕФЁАЭъУРѓнаЮЁБга ИіЃЈАќКЌЫФБпаЮABCDЃЉЃЎ
ЭиеЙЬсЩ§ЃК
ЃЈ4ЃЉЕБЭМЂлжаЕФЁЯBCD=90ЁуЪБЃЌСЌНгABЁфЃЌЧыЬНЧѓЁЯABЁфEЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉе§ЗНаЮЃЛЃЈ2ЃЉ80ЃЛЃЈ3ЃЉ5ЃЛЃЈ4ЃЉ45ЁуЃЎ
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉНсКЯЦНааЫФБпаЮЁЂОиаЮЁЂСтаЮЁЂе§ЗНаЮЕФаджЪКЭЁАЭъУРѓнаЮЁБЕФЖЈвхПЩвдЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШжЄЁЯAEBЁф=ЁЯBCBЁфЃЌдйЫуГіЁЯBCE=ЁЯECF=40ЁуЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉгЩелЕўЕФаджЪЕУГіBE=BЁфEЃЌBC=BЁфCЃЌЁЯB=ЁЯCBЁфE=90ЁуЃЌCD=CDЁфЃЌFD=FDЁфЃЌЁЯD=ЁЯCDЁфF=90ЁуЃЌМДПЩЕУГіЫФБпаЮEBCBЁфЁЂЫФБпаЮFDCDЁфЪЧЁАЭъУРѓнаЮЁБЃЌгЩЬтвтЕУГіЁЯODЁфE=ЁЯOBЁфF=90ЁуЃЌCDЁф=CBЁфЃЌгЩСтаЮЕФаджЪЕУГіAE=AFЃЌCE=CFЃЌдйжЄУїЁїOEDЁфЁеЁїOFBЁфЃЌЕУГіODЁф=OBЁфЃЌOE=OFЃЌжЄГіЁЯAEBЁф=ЁЯAFDЁф=90ЁуЃЌМДПЩЕУГіЫФБпаЮCDЁфOBЁфЁЂЫФБпаЮAEOFЪЧЁАЭъУРѓнаЮЁБЃЛМДПЩЕУГіНсТлЃЛ
ЃЈ4ЃЉЕБЭМЂлжаЕФЁЯBCD=90ЁуЪБЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌжЄУїAЁЂEЁЂBЁфЁЂFЫФЕуЙВдВЃЌЕУЕН![]() ЃЌгЩдВжмНЧЖЈРэМДПЩЕУЕНЁЯABЁфEЕФЖШЪ§ЃЎ
ЃЌгЩдВжмНЧЖЈРэМДПЩЕУЕНЁЯABЁфEЕФЖШЪ§ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЁрAB=CDЃЌAD=BCЃЌЁЯA=ЁЯCЁй90ЁуЃЌЁЯB=ЁЯDЁй90ЁуЃЌЁрABЁйADЃЌBCЁйCDЃЌЁрЦНааЫФБпаЮВЛвЛЖЈЮЊЁАЭъУРѓнаЮЁБЃЛ
ЂкЁпЫФБпаЮABCDЪЧОиаЮЃЌЁрЁЯA=ЁЯB=ЁЯC=ЁЯD=90ЁуЃЌAB=CDЃЌAD=BCЃЌЁрABЁйADЃЌBCЁйCDЃЌЁрОиаЮВЛвЛЖЈЮЊЁАЭъУРѓнаЮЁБЃЛ
ЂлЁпЫФБпаЮABCDЪЧСтаЮЃЌЁрAB=BC=CD=ADЃЌЁЯA=ЁЯCЁй90ЁуЃЌЁЯB=ЁЯDЁй90ЁуЃЌЁрСтаЮВЛвЛЖЈЮЊЁАЭъУРѓнаЮЁБЃЛ
ЂмЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрЁЯA=ЁЯB=ЁЯC=ЁЯD=90ЁуЃЌAB=BC=CD=ADЃЌЁре§ЗНаЮвЛЖЈЮЊЁАЭъУРѓнаЮЁБЃЛ
ЁрдкЦНааЫФБпаЮЁЂОиаЮЁЂСтаЮЁЂе§ЗНаЮЫФжжЭМаЮжаЃЌвЛЖЈЮЊЁАЭъУРѓнаЮЁБЕФЪЧе§ЗНаЮЃЛЙЪД№АИЮЊЃКе§ЗНаЮЃЛ
ЃЈ2ЃЉИљОнЬтвтЕУЃКЁЯBЁф=ЁЯB=90ЁуЃЌЁрдкЫФБпаЮCBEBЁфжаЃЌЁЯBEBЁф+ЁЯBCBЁф=180ЁуЃЌЁпЁЯAEBЁф+ЁЯBEBЁф=180ЁуЃЌЁрЁЯAEBЁф=ЁЯBCBЁфЃЌЁпЁЯBCE=ЁЯECF=ЁЯFCDЃЌЁЯBCD=120ЁуЃЌЁрЁЯBCE=ЁЯECF=40ЁуЃЌЁрЁЯAEBЁф=ЁЯBCBЁф=40Ёу+40Ёу=80ЁуЃЛЙЪД№АИЮЊЃК80ЃЛ
ЃЈ3ЃЉЕБЭМЂкжаЕФЫФБпаЮAECFЮЊСтаЮЪБЃЌЖдгІЭМЂлжаЕФЁАЭъУРѓнаЮЁБга5ИіЃЛРэгЩШчЯТЃЛ
ИљОнЬтвтЕУЃКBE=BЁфEЃЌBC=BЁфCЃЌЁЯB=ЁЯCBЁфE=90ЁуЃЌCD=CDЁфЃЌFD=FDЁфЃЌЁЯD=ЁЯCDЁфF=90ЁуЃЌЁрЫФБпаЮEBCBЁфЁЂЫФБпаЮFDCDЁфЪЧЁАЭъУРѓнаЮЁБЃЛ
ЁпЫФБпаЮABCDЪЧЁАЭъУРѓнаЮЁБЃЌЁрAB=ADЃЌCB=CDЃЌЁЯB=ЁЯD=90ЁуЃЌЁрCDЁф=CBЁфЃЌЁЯCDЁфO=ЁЯCBЁфO=90ЁуЃЌЁрЁЯODЁфE=ЁЯOBЁфF=90ЁуЃЌЁпЫФБпаЮAECFЮЊСтаЮЃЌЁрAE=AFЃЌCE=CFЃЌAEЁЮCFЃЌAFЁЮCEЃЌЁрDЁфE=BЁфFЃЌЁЯAEBЁф=ЁЯCBЁфE=90ЁуЃЌЁЯAFDЁф=ЁЯCDЁфF=90ЁуЃЌдкЁїOEDЁфКЭЁїOFBЁфжаЃЌЁпЁЯODЁфE=ЁЯOBЁфFЃЌЁЯEODЁф=ЁЯFOBЁфЃЌDЁфE=BЁфFЃЌЁрЁїOEDЁфЁеЁїOFBЁфЃЈAASЃЉЃЌЁрODЁф=OBЁфЃЌOE=OFЃЌЁрЫФБпаЮCDЁфOBЁфЁЂЫФБпаЮAEOFЪЧЁАЭъУРѓнаЮЁБЃЛ
ЁрАќКЌЫФБпаЮABCDЃЌЖдгІЭМЂлжаЕФЁАЭъУРѓнаЮЁБга5ИіЃЛЙЪД№АИЮЊЃК5ЃЛ
ЃЈ4ЃЉЕБЭМЂлжаЕФЁЯBCD=90ЁуЪБЃЌШчЭМЫљЪОЃКЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрЁЯA=90ЁуЃЌЁпЁЯEBЁфF=90ЁуЃЌЁрЁЯA+ЁЯEBЁфF=180ЁуЃЌЁрAЁЂEЁЂBЁфЁЂFЫФЕуЙВдВЃЌЁпAE=AFЃЌЁр![]() ЃЌЁрЁЯABЁфE=ЁЯABЁфF=
ЃЌЁрЁЯABЁфE=ЁЯABЁфF=![]() ЁЯEBЁфF=45ЁуЃЎ
ЁЯEBЁфF=45ЁуЃЎ


 ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ
ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ БІБДМЦЛЎЦкФЉГхДЬЖс100ЗжЯЕСаД№АИ
БІБДМЦЛЎЦкФЉГхДЬЖс100ЗжЯЕСаД№АИ ФмПМЪдШЋФм100ЗжЯЕСаД№АИ
ФмПМЪдШЋФм100ЗжЯЕСаД№АИ