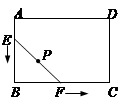题目内容

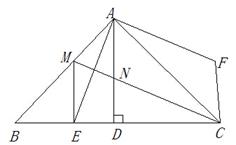
如图，在矩形ABCD内，以BC为一边作等边三角形EBC，连接AE，DE．若BC＝2，ED＝，则AB的长为（   ）
A．2B．2C．＋D．2＋
C．

试题分析：过E作EF⊥AD，

∵四边形ABCD是矩形，
∴AD∥BC，
∴EG⊥BC，
∵△BEC为边长2的等边三角形，
∴EB=2，BG=1，
根据勾股定理得：EG=，
由对称性得到△AED为等腰三角形，即AE=DE，
∵DE=，FD=AD=1，
∴根据勾股定理得：EF=，
则AB=FG=FE+EG=+．
故选C．
练习册系列答案
相关题目
已知：如图，在△DBC中，BC=DC,过点C作CE⊥DC交DB的延长线于点E，过点C作AC⊥BC且AC=EC，连结AB．
求证：AB=ED.
面给出的三块正方形纸板的边长都是60cm，请分别按下列要求设计一种剪裁方法，折叠成一个礼品包装盒（纸板的厚度忽略不计）．要求尽可能多地利用纸板，用虚线表示你的设计方案，并把剪裁线用实线标出．
（1）包装礼盒的六个面由六个矩形组成（如图1），请画出对应的设计图．
                
图1
（2）包装礼盒的上盖由四个全等的等腰直角三角形组成（如图2），请画出对应的设计图．
                   
图2               
（3）包装礼盒的上盖是双层的，由四个全等的矩形组成（如图3），请画出对应的设计图．
  
图3
如图，AC交BD于点O，请你从三项中选出两个作为条件，另一个作为结论，写出一个真命题，并加以证明.
①OA=OC   ②OB=OD    ③AB∥CD
如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E.在△ABC外有一点F，使FA⊥AE，FC⊥BC.
（1）求证：BE=CF；
（2）在AB上取一点M，使BM=2DE，连接MC，交AD于点N，连接ME.求证：①ME⊥BC；②DE=DN.
矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　  　．
在矩形ABCD中，已知AB=2cm，BC=3cm，现有一根长为2 cm的木棒EF紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则木棒EF的中点P在运动过程中所围成的图形的面积为（ ）
A．6 cm2B．3 cm2C．（2＋π）cm2D．（6－π）cm2
如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿AD对折点C落在C1位置，则BC1和BC之间数量关系是          。
已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若BD+CE=5，则线段DE的长为    (   )
A．5      B．6      C．7      D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网