题目内容
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD。
求证:(1)BD=CE (7分)
(2)BD⊥CE(5分)
证明:(1)∵△ACB和△ADE是等腰三角形, BAC=
BAC= DAE=90º
DAE=90º
∴AB=AC,AD=AE …………(1分)
 BAC+
BAC+ CAD=
CAD= DAE+
DAE+ CAD …………(2分)
CAD …………(2分)
即 BAD=
BAD= CAE …………(3分)
CAE …………(3分)
在△ABD与△ACE中
∵ 
∴△ABD≌△ACE(SAS) …………(6分)
∴BD=CE …………(7分)
(2)∵△ADE是等腰直角三角形, DAE=90º
DAE=90º
∴ E=
E= ADE=45º …………(1分)
ADE=45º …………(1分)
又∵△ABD≌△ACE
∴ ADB=
ADB= E=45º …………(3分)
E=45º …………(3分)
∴ BDE=
BDE= ADB+
ADB+ ADE=45º+45º=90º …………(4分)
ADE=45º+45º=90º …………(4分)
∴BD CE
CE

练习册系列答案
相关题目


 ,然后选取一个使原式有意义的
,然后选取一个使原式有意义的 的
的
 B.
B. C.
C. D.
D.
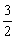 sin30°<x<sin60°;B.cos30°<x<
sin30°<x<sin60°;B.cos30°<x< 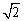 cos45°;
cos45°;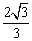 tan60°。
tan60°。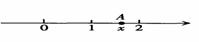
 B.
B. C.
C. D.
D.