ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ”––μΕύ¥ζ ΐΚψΒ» ΫΩ…“‘”ΟΆΦ–ΈΒΡΟφΜΐά¥±μ ΨΘ§»γΆΦ![]() Θ§Υϋ±μ ΨΝΥ
Θ§Υϋ±μ ΨΝΥ![]()
![]() ΆΦ
ΆΦ![]() «ΫΪ“ΜΗω≥Λ2mΓΔΩμ2nΒΡ≥ΛΖΫ–ΈΘ§―ΊΆΦ÷––ιœΏΤΫΖΫΈΣΥΡΩι–Γ≥ΛΖΫ–ΈΘ§»ΜΚσ‘ΌΤ¥≥…“ΜΗω’ΐΖΫ–Έ
«ΫΪ“ΜΗω≥Λ2mΓΔΩμ2nΒΡ≥ΛΖΫ–ΈΘ§―ΊΆΦ÷––ιœΏΤΫΖΫΈΣΥΡΩι–Γ≥ΛΖΫ–ΈΘ§»ΜΚσ‘ΌΤ¥≥…“ΜΗω’ΐΖΫ–Έ![]() ΆΦ
ΆΦ![]() Θ§‘ρΆΦ
Θ§‘ρΆΦ![]() ÷–ΒΡ“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΒ»”Ύ______
÷–ΒΡ“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΒ»”Ύ______![]() ”ΟΚ§mΓΔnΒΡ¥ζ ΐ Ϋ±μ Ψ
”ΟΚ§mΓΔnΒΡ¥ζ ΐ Ϋ±μ Ψ![]()
![]() «κ”ΟΝΫ÷÷≤ΜΆ§ΒΡΖΫΖ®Ν–¥ζ ΐ Ϋ±μ ΨΆΦ
«κ”ΟΝΫ÷÷≤ΜΆ§ΒΡΖΫΖ®Ν–¥ζ ΐ Ϋ±μ ΨΆΦ![]() ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
ΖΫΖ®![]() ______ΖΫΖ®
______ΖΫΖ®![]() ______
______
![]() «κΡψΙέ≤λΆΦ–Έ
«κΡψΙέ≤λΆΦ–Έ![]() Θ§–¥≥ω»ΐΗω¥ζ ΐ Ϋ
Θ§–¥≥ω»ΐΗω¥ζ ΐ Ϋ![]() ΓΔ
ΓΔ![]() ΓΔmnΙΊœΒΒΡΒ» ΫΘΚ______ΘΜ
ΓΔmnΙΊœΒΒΡΒ» ΫΘΚ______ΘΜ
![]() ΗυΨί
ΗυΨί![]() Χβ÷–ΒΡΒ»ΝΩΙΊœΒΘ§ΫβΨω»γœ¬Έ ΧβΘΚ»τ“―÷Σ
Χβ÷–ΒΡΒ»ΝΩΙΊœΒΘ§ΫβΨω»γœ¬Έ ΧβΘΚ»τ“―÷Σ![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ______ΘΜ
______ΘΜ
![]() –ΓΟς”Ο8Ηω“Μ―υ¥σΒΡ≥ΛΖΫ–Έ
–ΓΟς”Ο8Ηω“Μ―υ¥σΒΡ≥ΛΖΫ–Έ![]() ≥ΛacmΘ§Ωμ
≥ΛacmΘ§Ωμ![]() Τ¥ΆΦΘ§Τ¥≥ωΝΥ»γΆΦΦΉΓΔ““ΒΡΝΫ÷÷ΆΦΑΗΘ§ΆΦΑΗΦΉ «“ΜΗω’ΐΖΫ–ΈΘ§ΆΦΑΗ““ «“ΜΗω¥σΒΡ≥ΛΖΫ–ΈΘ§ΆΦΑΗΦΉΒΡ÷–ΦδΝτœ¬ΝΥ±Ώ≥Λ «2cmΒΡ’ΐΖΫ–Έ–ΓΕ¥
Τ¥ΆΦΘ§Τ¥≥ωΝΥ»γΆΦΦΉΓΔ““ΒΡΝΫ÷÷ΆΦΑΗΘ§ΆΦΑΗΦΉ «“ΜΗω’ΐΖΫ–ΈΘ§ΆΦΑΗ““ «“ΜΗω¥σΒΡ≥ΛΖΫ–ΈΘ§ΆΦΑΗΦΉΒΡ÷–ΦδΝτœ¬ΝΥ±Ώ≥Λ «2cmΒΡ’ΐΖΫ–Έ–ΓΕ¥![]() ‘ρ
‘ρ![]() ΒΡ÷ΒΈΣ______Θ°
ΒΡ÷ΒΈΣ______Θ°
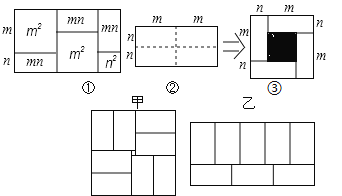
ΓΨ¥πΑΗΓΩΘ®1Θ©m-nΘΜΘ®2Θ©![]() ΘΜ
ΘΜ![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() ΘΜΘ®4Θ©9ΘΜΘ®5Θ©4.
ΘΜΘ®4Θ©9ΘΜΘ®5Θ©4.
ΓΨΫβΈωΓΩ
![]() “θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ
“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() ΘΜ
ΘΜ
![]() ΖΫΖ®
ΖΫΖ®![]() ΘΚ“θ”Α≤ΩΖ÷ΒΡΟφΜΐ
ΘΚ“θ”Α≤ΩΖ÷ΒΡΟφΜΐ![]() ¥σ’ΐΖΫ–ΈΒΡΟφΜΐ
¥σ’ΐΖΫ–ΈΒΡΟφΜΐ![]() Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΘΜΖΫΖ®
Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΘΜΖΫΖ®![]() ΘΚ±μ Ψ≥ω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ
ΘΚ±μ Ψ≥ω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() Θ§Φ¥Ω…Ϋβ¥πΘΜ
Θ§Φ¥Ω…Ϋβ¥πΘΜ
![]() ¥σ’ΐΖΫ–ΈΒΡΟφΜΐΦθ»Ξ4Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΦ¥Ω…ΒΟ≥ω“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ§“≤Ω…ΒΟ≥ω»ΐΗω¥ζ ΐ Ϋ
¥σ’ΐΖΫ–ΈΒΡΟφΜΐΦθ»Ξ4Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΦ¥Ω…ΒΟ≥ω“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ§“≤Ω…ΒΟ≥ω»ΐΗω¥ζ ΐ Ϋ![]() ΓΔ
ΓΔ![]() ΓΔmn÷°ΦδΒΡΒ»ΝΩΙΊœΒΘΜ
ΓΔmn÷°ΦδΒΡΒ»ΝΩΙΊœΒΘΜ
![]() ΗυΨί
ΗυΨί![]() ΥυΒΟ≥ωΒΡΙΊœΒ ΫΘ§Ω…«σ≥ω
ΥυΒΟ≥ωΒΡΙΊœΒ ΫΘ§Ω…«σ≥ω![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
![]() άϊ”ΟΆΦ–ΈΟφΜΐ÷°ΦδΙΊœΒΒΟ≥ω
άϊ”ΟΆΦ–ΈΟφΜΐ÷°ΦδΙΊœΒΒΟ≥ω![]() Φ¥Ω…«σ≥ωΘ°
Φ¥Ω…«σ≥ωΘ°
![]() “θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ
“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
![]() ΖΫΖ®
ΖΫΖ®![]() ΘΚ“θ”Α≤ΩΖ÷ΒΡΟφΜΐ
ΘΚ“θ”Α≤ΩΖ÷ΒΡΟφΜΐ![]() ¥σ’ΐΖΫ–ΈΒΡΟφΜΐ
¥σ’ΐΖΫ–ΈΒΡΟφΜΐ![]() Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΘ§
Ηω–Γ≥ΛΖΫ–ΈΒΡΟφΜΐΘ§
Υυ“‘“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣΘΚ![]() ΘΜ
ΘΜ
ΖΫΖ®![]() ΘΚ±μ Ψ≥ω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ
ΘΚ±μ Ψ≥ω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() Θ§
Θ§
Υυ“‘“θ”Α≤ΩΖ÷ΒΡΟφΜΐ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ![]() Θ°
Θ°
![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ9Θ°
![]() Θ§
Θ§
![]() ΒΡ÷ΒΈΣ4Θ°
ΒΡ÷ΒΈΣ4Θ°
Ι ¥πΑΗΈΣΘΚ4Θ°





