题目内容
如图，在四边形ABCD中，AB=
，BC=1，CD=3，∠B=135°，∠C=90°，则∠D等于
- A.60°
- B.67.5°
- C.75°
- D.无法确定
B
分析：通过对内分割或向外补形，构造直角三角形，解出AF、BF的长，得出AE、DE，解直角三角形ADE求出角D的度数．
解答：
解：如图所示
过A作AE⊥CD于E，B作BF⊥AE于F．
∵∠B=135，∠C=90
∴∠BAF=45°．
∴AF=BF=
=
∴AE=AF+BC=2
，DE=3-BF=4-2
得tan∠D=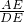
=
．
故∠D=67.5°．
故选B．
点评：考查了解直角三角形的应用．
注：因直角三角形元素之间有很多关系，故用已知元素与未知元素的途径常不惟一，选择怎样的途径最有效、最合理呢？请记住：有斜用弦，无斜用切，宁乘勿除．在没有直角的条件下，常通过作垂线构造直角三角形；在解由多个直角三角形组合而成的问题时，往往先解已具备条件的直角三角形，使得求解的直角三角形最终可解．
分析：通过对内分割或向外补形，构造直角三角形，解出AF、BF的长，得出AE、DE，解直角三角形ADE求出角D的度数．
解答：
解：如图所示过A作AE⊥CD于E，B作BF⊥AE于F．
∵∠B=135，∠C=90
∴∠BAF=45°．
∴AF=BF=
=∴AE=AF+BC=2
，DE=3-BF=4-2得tan∠D=
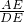=．故∠D=67.5°．
故选B．
点评：考查了解直角三角形的应用．
注：因直角三角形元素之间有很多关系，故用已知元素与未知元素的途径常不惟一，选择怎样的途径最有效、最合理呢？请记住：有斜用弦，无斜用切，宁乘勿除．在没有直角的条件下，常通过作垂线构造直角三角形；在解由多个直角三角形组合而成的问题时，往往先解已具备条件的直角三角形，使得求解的直角三角形最终可解．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
（2013•赤峰）如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
已知：如图，在四边形ABC中，AD=BC，AB=CD．
如图，在Rt△ABC中，∠BAC=90°，将△ABC沿线段BC向右平移得到△DEF，使CE=AE，连结AD、AE、CD，则下列结论：①AD∥BE且AD=BE；②∠ABC=∠DEF；③ED⊥AC；④四边形AECD为菱形，其中正确的共有（ ）
已知：如图，在四边形ABC中，AD=BC，AB=CD．