题目内容
如图,在等腰△ABC中,AB=AC=5cm,BC=6cm,点P从点B开始沿BC边以每秒1cm的速度向点C运动,点Q从点C开始沿CA边以每秒2 cm的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P,Q分别从B,C两点同时出发,当点Q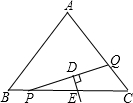 运动到点A时,点Q、p停止运动,设它们运动的时间为x cm.
运动到点A时,点Q、p停止运动,设它们运动的时间为x cm.(1)当x=
(2)当点Q运动时,设四边形ABPQ的面积为ycm2,求y与x的函数关系式(不用写出自变量取值范围);
(3)当点Q运动时,是否存在以P、Q、C为顶点的三角形与△PDE相似?若存在,求出x的值;若不存在,请说明理由.
分析:(1)由于DE垂直平分PQ,所以只要CP=CQ,根据等腰三角形的性质,DE又是顶角的平分线,所以列出方程,求出x=2.
(2)由于四边形AQPB的形状不规则,所以可以用△ABC的面积减去△PQC的面积,而△PQC的面积可以用x表达,则四边形AQPB的面积也可以用x表达出来.
(3)假设存在,根据已知条件,易证△PQC∽△AMC,所以
=
,所以
=
,即x=
.
(2)由于四边形AQPB的形状不规则,所以可以用△ABC的面积减去△PQC的面积,而△PQC的面积可以用x表达,则四边形AQPB的面积也可以用x表达出来.
(3)假设存在,根据已知条件,易证△PQC∽△AMC,所以
| QC |
| MC |
| PC |
| AC |
| 2x |
| 3 |
| 6-x |
| 5 |
| 18 |
| 13 |
解答: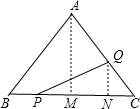 解:(1)x=2;
解:(1)x=2;
当DE经过点C时,∵DE⊥PQ,PD=QD,
∴PC=CQ,PC=6-x,CQ=2x,
即6-x=2x,得x=2,
∴当x=2时,当DE经过点C;
(2)分别过点Q、A作QN⊥BC,AM⊥BC垂足为M、N.
∵AB=AC=5cm,BC=6cm,
∴AM=
=4(cm),
∵QN∥AM,
∴△QNC∽△AMC,
∴
=
,即
=
,
∴QN=
x,
又PC=6-x,
∴S△PCQ=
PC•QN=
(6-x)•
x,
∴y=S△ABC-S△PCQ=
×6×4-
(6-x)•
x,
即y=
x2-
x+12;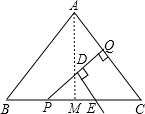
(3)存在.
理由如下:
∵DE⊥PQ,
∴PQ⊥AC时△PQC∽△PDE
此时,△PQC∽△AMC
∴
=
即
=
∴x=
.
 解:(1)x=2;
解:(1)x=2;当DE经过点C时,∵DE⊥PQ,PD=QD,
∴PC=CQ,PC=6-x,CQ=2x,
即6-x=2x,得x=2,
∴当x=2时,当DE经过点C;
(2)分别过点Q、A作QN⊥BC,AM⊥BC垂足为M、N.
∵AB=AC=5cm,BC=6cm,
∴AM=
| 52-32 |
∵QN∥AM,
∴△QNC∽△AMC,
∴
| QN |
| AM |
| CQ |
| CA |
| QN |
| 4 |
| 2x |
| 5 |
∴QN=
| 8 |
| 5 |
又PC=6-x,
∴S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
∴y=S△ABC-S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
即y=
| 4 |
| 5 |
| 24 |
| 5 |

(3)存在.
理由如下:
∵DE⊥PQ,
∴PQ⊥AC时△PQC∽△PDE
此时,△PQC∽△AMC
∴
| QC |
| MC |
| PC |
| AC |
| 2x |
| 3 |
| 6-x |
| 5 |
∴x=
| 18 |
| 13 |
点评:本题需先证得三角形相似和待定系数法求二次函数解析式,再通过相似形的性质,解决问题,全面的考查了相似形的性质和判定.

练习册系列答案
相关题目
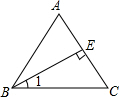 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
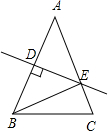 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=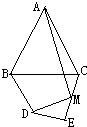 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.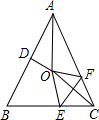 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是