题目内容
如图,在直径为AB的圆内,划出一块三角形区域使三角形的一边为AB,顶点C在半圆上,其他两边分别为6和8,现在建造一个内接内△ABC的矩形水池DEFN,其中DE在AB上,如图的设计方案是AC=8,BC=6.
?
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x为何值时,水池DEFN的面积最大?
(3)实施施工时,发现在AB边上距B点1.85m处的M处有一棵大树,这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开这棵大树.
答案:
解析:
解析:
|
(1)作CH⊥AB于H交NF于G,则CH=h ∵∠ACB= S△ABC= ∴h=4.8
(2)设矩形面积为S ∵△CNT∽△CAB ∴ ∴ ∴NF= ∴S=x ∴当x=2.4时,矩形DEFN的面积最大 (3)∵ ∴CF= ∴BF=3 在Rt△BEF中,根据勾股定理得,BE= ∵BM=1.85 ∴这棵大树位于最大矩形的边上 为了保护大树,在半圆上取点 |

练习册系列答案
相关题目

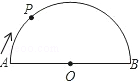
 (2013•贵阳)如图,在直径为AB的半圆O上有一动点P从A点出发,按顺时针方向绕半圆匀速运动到B点,然后再以相同的速度沿着直径回到A点停止,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
(2013•贵阳)如图,在直径为AB的半圆O上有一动点P从A点出发,按顺时针方向绕半圆匀速运动到B点,然后再以相同的速度沿着直径回到A点停止,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )

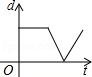 B.
B.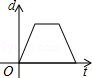 C.
C.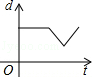 D.
D.