题目内容
18.解方程组:$\left\{\begin{array}{l}{x+y-z=6}\\{x-3y+2z=1}\\{3x+2y-z=3}\end{array}\right.$.分析 ①-③消去z得到一个方程,记作④,①×2+②消去z得到另一个方程,记作⑤,两方程联立求出x、y的值,把x、y的值代入①即可得到原方程组的解.
解答 解:$\left\{\begin{array}{l}{x+y-z=6①}\\{x-3y+2z=1②}\\{3x+2y-z=3③}\end{array}\right.$,
①-③得:-2x-y=3④,
①×2+②得:3x-y=13⑤,
两方程联立得:$\left\{\begin{array}{l}{-2x-y=3④}\\{3x-y=13⑤}\end{array}\right.$,
⑤-④得:5x=10,
解得:x=2,
把x=2代入④得:y=-7,
把x=2,y=-7代入①得:z=-11,
所以方程组的解是:$\left\{\begin{array}{l}{x=2}\\{y=-7}\\{z=-11}\end{array}\right.$.
点评 此题考查了三元一次方程组的解法,利用了消元的思想,消元的方法有两种:加减消元法;代入消元法,熟练掌握两种方法是解本题的关键.

练习册系列答案
相关题目

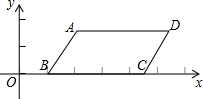 如图,在平行四边形ABCD中,已知A、B、C三点坐标分别为A(1+$\sqrt{3}$,$\sqrt{3}$),B(1,0),C(1+2$\sqrt{3}$,0)
如图,在平行四边形ABCD中,已知A、B、C三点坐标分别为A(1+$\sqrt{3}$,$\sqrt{3}$),B(1,0),C(1+2$\sqrt{3}$,0)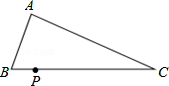 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中准确的是( )
如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中准确的是( )


