题目内容
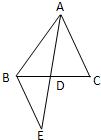15、如图，延长△ABC的中线AD至E，使DE=AD，连接BE，则△ADC≌△EDB，其中所使用的判定方法为SAS
，BE与AC的位置关系是平行
．分析：由于ED=AD，∠ADC=∠EDB，BD=CD，所以利用SAS可证△ADC≌△EDB，再利用全等三角形的性质，可知∠ACD=∠EBD，所以AC∥BE．
解答：证明：∵AD是△ABC的中线，
∴BD=CD，
又∵∠ADC=∠EDB，AD=ED，
∴△ADC≌△EDB （SAS）
∴∠ACD=∠EBD，
∴AC∥BE．
故填SAS，平行．
∴BD=CD，
又∵∠ADC=∠EDB，AD=ED，
∴△ADC≌△EDB （SAS）
∴∠ACD=∠EBD，
∴AC∥BE．
故填SAS，平行．
点评：本题利用了全等三角形的判定和性质、平行线的判定的知识．做题时要结合图形进行思考．
练习册系列答案
相关题目
21、已知，如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接D，E，F，得到△DEF为等边三角形．
6、如图，延长△ABC的边BA到E，D是AC上任意一点，则下列不等关系中一定成立的是（ ）
如图，延长△ABC的边BC到D，使CD=BC，取AB中点F，边DF交AC于E，求
已知，如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接D，E，F，得到△DEF为等边三角形．求证：