题目内容
如图,抛物线y=mx2+3mx-3(m>0)与y轴交于点C,与x轴交于A、B两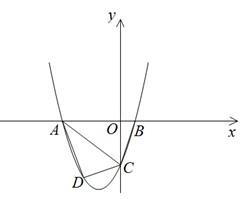 点,点A在点B的左侧,且tan∠OCB=
点,点A在点B的左侧,且tan∠OCB=| 1 | 3 |
(1)求此抛物线的解析式;
(2)如果点D是线段AC下方抛物线上的动点,设D点的横坐标为x,△ACD的面积为S,求S与x的关系式,并求当S最大时点D的坐标;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点的平行四边形?若存在求点P坐标;若不存在,请说明理由.
分析:(1)由抛物线解析式可求C(0,-3),在Rt△BOC中,已知tan∠OCB=
,OC=3,可求OB,确定B点坐标,代入抛物线解析式求m即可;
(2)依题意可知,点D(x,
x2+
x-3),连接OD,由S△ACD=S△AOD+S△DOC-S△AOC,求S的表达式,利用配方法求S的最大值及此时D点坐标;
(3)存在.分三种情况:①当以AC为边,CP也是平行四边形的边;②当以AC为对角线,CP为边;③当以AC为边,CP是平行四边形的对角线;结合图形的性质分别求解.
| 1 |
| 3 |
(2)依题意可知,点D(x,
| 3 |
| 4 |
| 9 |
| 4 |
(3)存在.分三种情况:①当以AC为边,CP也是平行四边形的边;②当以AC为对角线,CP为边;③当以AC为边,CP是平行四边形的对角线;结合图形的性质分别求解.
解答: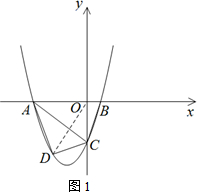 解:(1)由抛物线y=mx2+3mx-3,得C(0,-3),
解:(1)由抛物线y=mx2+3mx-3,得C(0,-3),
∵tan∠OCB=
,∠COB=90°,
∴
=
,∴B(1,0),
∵抛物线y=mx2+3mx-3(m>0)过点B,
∴m+3m-3=0,∴m=
,
∴抛物线的解析式为y=
x2+
x-3;
(2)如图1,∵抛物线对称轴为x=-
,B(1,0),∴A(-4,0)连接OD,
∵点D在抛物线y=
x2+
x-3上,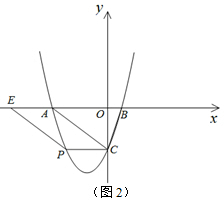
∴设点D(x,
x2+
x-3),
则S△ACD=S△AOD+S△DOC-S△AOC
=
×4(-
x2-
x+3)+
×3(-x)-
×4×3
=-
x2-6x,
∴S=-
(x+2)2+6,
∴当x=-2时,△ACD的面积S有最大值为6.
此时,点D的坐标为(-2,-
).
(3)①如图2,当以AC为边,CP也是平行四边形的边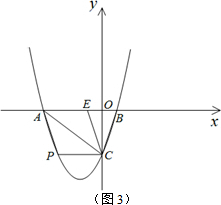 时,CP∥AE,点P与点C关于抛物线的对称轴对称,此时P(-3,-3).
时,CP∥AE,点P与点C关于抛物线的对称轴对称,此时P(-3,-3).
②如图3,当以AC为对角线,CP为边时,此时P点的坐标是(-3,-3).
③如图4、图5,当以AC为边,CP是平行四边形的对角线时,点P、C到x轴的距离相等,
则
x2+
x-3=3,解得x=
,
此时P(
,3)(如图4),或(
,3)(如图5),
综上所述,存在三个点符合题意,分别是P1(-3,-3),P2(
,3),P3(
,3).
 解:(1)由抛物线y=mx2+3mx-3,得C(0,-3),
解:(1)由抛物线y=mx2+3mx-3,得C(0,-3),∵tan∠OCB=
| 1 |
| 3 |
∴
| OB |
| OC |
| 1 |
| 3 |
∵抛物线y=mx2+3mx-3(m>0)过点B,
∴m+3m-3=0,∴m=
| 3 |
| 4 |
∴抛物线的解析式为y=
| 3 |
| 4 |
| 9 |
| 4 |
(2)如图1,∵抛物线对称轴为x=-
| 3 |
| 2 |
∵点D在抛物线y=
| 3 |
| 4 |
| 9 |
| 4 |

∴设点D(x,
| 3 |
| 4 |
| 9 |
| 4 |
则S△ACD=S△AOD+S△DOC-S△AOC
=
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
∴S=-
| 3 |
| 2 |
∴当x=-2时,△ACD的面积S有最大值为6.
此时,点D的坐标为(-2,-
| 9 |
| 2 |
(3)①如图2,当以AC为边,CP也是平行四边形的边
 时,CP∥AE,点P与点C关于抛物线的对称轴对称,此时P(-3,-3).
时,CP∥AE,点P与点C关于抛物线的对称轴对称,此时P(-3,-3).②如图3,当以AC为对角线,CP为边时,此时P点的坐标是(-3,-3).
③如图4、图5,当以AC为边,CP是平行四边形的对角线时,点P、C到x轴的距离相等,
则
| 3 |
| 4 |
| 9 |
| 4 |
-3±
| ||
| 2 |
此时P(
-3-
| ||
| 2 |
-3+
| ||
| 2 |
综上所述,存在三个点符合题意,分别是P1(-3,-3),P2(
-3-
| ||
| 2 |
-3+
| ||
| 2 |

点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.
如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.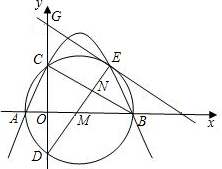 已知:如图,抛物线
已知:如图,抛物线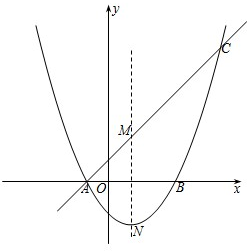 如图,抛物线y=
如图,抛物线y=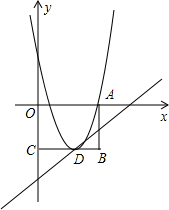 (2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.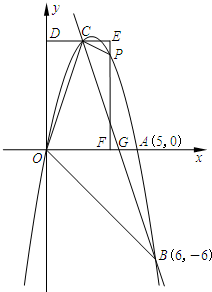 如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.
如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.