题目内容
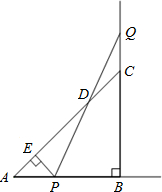 如图所示,等腰直角三角形△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度做直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线AC相交于点D.
如图所示,等腰直角三角形△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度做直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线AC相交于点D.(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式.
(2)当AP的长为何值时S△PCQ=S△ABC.
分析:(1)由条件可以得出AP=CQ,就有BQ=x+2,PB=2-x或x-2,分两种情况讨论,0≤x≤2,和x>2时由三角形的面积公式及可以求出结论;
(2)先求出△ABC的面积,根据(1)的解析式分别建立方程求出其值即可.
(2)先求出△ABC的面积,根据(1)的解析式分别建立方程求出其值即可.
解答:解:(1)∵△ABC是等腰直角三角形,
∴AB=BC=2.
∵P、Q速度相同,
∴AP=CQ=x,
当0≤x≤2时
S=
=-
x2+x
当x>2时,
S=
=
x2-x,
∴S=
;
(2)由题意,得
当-
x2+x=2时,
△<0,原方程无解;
x2-x=2时
解得:x1=1+
,x2=1-
(舍去)
∴AP=1+
.
答:当AP=1+
时,S△PCQ=S△ABC.
∴AB=BC=2.
∵P、Q速度相同,
∴AP=CQ=x,
当0≤x≤2时
S=
| x(2-x) |
| 2 |
| 1 |
| 2 |
当x>2时,
S=
| x(x-2) |
| 2 |
| 1 |
| 2 |
∴S=
|
(2)由题意,得
当-
| 1 |
| 2 |
△<0,原方程无解;
| 1 |
| 2 |
解得:x1=1+
| 5 |
| 5 |
∴AP=1+
| 5 |
答:当AP=1+
| 5 |
点评:本题考查了二次函数的解析式的运用,三角形的面积公式的运用,一元二次方程的解法的运用,解答时求出二次函数解析式是关键.

练习册系列答案
相关题目
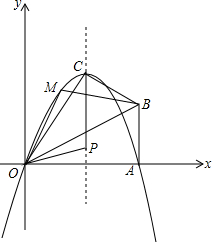 (2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.