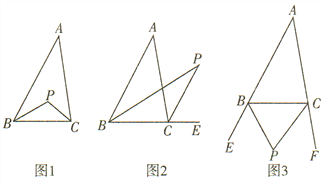
题目内容
【题目】在△ABC中,∠A=40°.
(1)如图1,若两内角∠ABC,∠ACB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(2)如图2,若内角∠ABC,外角∠ACE的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(3)如图3,若两外角∠EBC,∠FCB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .
(选择其中一种数量关系加以证明)
【答案】(1)∠P=90°+![]() ∠A;(2)∠P=
∠A;(2)∠P=![]() ∠A;(3)70°;∠P=90°-∠A.
∠A;(3)70°;∠P=90°-∠A.
【解析】试题分析:(1)根据三角形内角和定理求出∠B和∠C,再根据角平分线的性质和三角形内角和是180°求出∠P=180°-![]() (∠B+∠C);
(∠B+∠C);
(2)根据三角形的一个外角等于和它不相邻的两个内角的和以及叫平分线的性质可求出∠P,可得∠A与∠P之间的数量关系;
(3)根据三角形的一个外角等于和它不相邻的两个内角的和求得:∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,在△BCP中根据角平分线的定义以及三角形内角和定理即可求解.
试题解析:(1)∠ABC+∠C=180°∠A=180°40°=140°
∴![]() (∠ABC+∠C)=
(∠ABC+∠C)=![]() ×140°=70°,
×140°=70°,
∴∠P=180°![]() (∠ABC+∠C)=110°.
(∠ABC+∠C)=110°.
∠A与∠P之间的数量关系是∠P=90°+![]() ∠A;
∠A;
(2)∵![]() ∠ACE=
∠ACE=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (40°+∠ABC)=
(40°+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴∠P=20°.
∠A与∠P之间的数量关系是∠P=![]() ∠A;
∠A;
(3)∵∠EBC=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,
∴∠PBC+∠PCB=90°+![]() ∠A.
∠A.
又∵∠PBC+∠PCB+∠P=180°,
∴90°+![]() ∠A+∠P=180°,即∠P=90°
∠A+∠P=180°,即∠P=90°![]() ∠A,
∠A,
当∠A=40°时,∠P=70°.