题目内容
(本题6分)如图,四边形 是正方形,点
是正方形,点 在
在 上,
上, ,垂足为
,垂足为 ,请你在
,请你在 上确定一点
上确定一点 ,使
,使
 ,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明
,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明 .
.

方案
一:  ;方案
;方案
二:(1)作法:(2) 证明:
 是正方形,点
是正方形,点 在
在 上,
上, ,垂足为
,垂足为 ,请你在
,请你在 上确定一点
上确定一点 ,使
,使
 ,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明
,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明 .
.
方案
|
 ;方案
;方案
|
解:方案
:(一)过点B作BG⊥AE,垂足为G;(二)在AE上截取AG=DF;
(三)作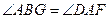 交AE于点G;…………………………2分
交AE于点G;…………………………2分
(注:其中任意一个均可作为方案一,另外再选择一个作为方案二)
(作法正确)……………………………………………………………………………3分
(2)①如果是过点B作BG⊥AE,垂足为G,证明如下:
∵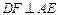 ,BG⊥AE,
,BG⊥AE,
∴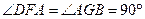 .…………
.………… …………………………………………………4分
…………………………………………………4分
由题意知,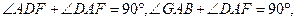
∴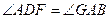 .……………………………………………………………………5分
.……………………………………………………………………5分
∵四边形 是正方形,∴AD=AB,
是正方形,∴AD=AB,
在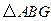 与
与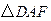 中,
中,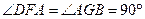 ,
,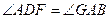 ,AD=AB,
,AD=AB,
∴ (AAS). ………………………………………………………6分
(AAS). ………………………………………………………6分
②如果是在AE上截取AG=DF,证明如下:
∵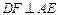 ,AD⊥AE,
,AD⊥AE,
∴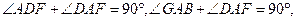
∴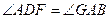 .……………………………………………………………………4分
.……………………………………………………………………4分
∵四边形 是正方形,∴AD=AB, …
是正方形,∴AD=AB, … …………………………………………5分
…………………………………………5分
在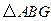 与
与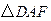 中,AG=DF,
中,AG=DF,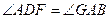 ,AD=AB,
,AD=AB,
∴ (SAS). ………………………………………………………6分
(SAS). ………………………………………………………6分
③如果作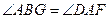 交AE于点G,证明如下:
交AE于点G,证明如下:
∵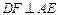 ,AD⊥AE,
,AD⊥AE,
∴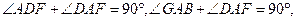
∴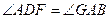 .……………………………………………………………………4分
.……………………………………………………………………4分
∵四边形 是正方形,∴AD=AB, ……………………………………………5分
是正方形,∴AD=AB, ……………………………………………5分
在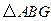 与
与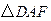 中,
中,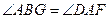 , AD=AB,
, AD=AB,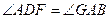
∴ (ASA). ………………………………………………………6分
(ASA). ………………………………………………………6分
|
(三)作
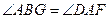 交AE于点G;…………………………2分
交AE于点G;…………………………2分(注:其中任意一个均可作为方案一,另外再选择一个作为方案二)
(作法正确)……………………………………………………………………………3分
(2)①如果是过点B作BG⊥AE,垂足为G,证明如下:
∵
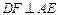 ,BG⊥AE,
,BG⊥AE,∴
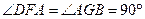 .…………
.………… …………………………………………………4分
…………………………………………………4分由题意知,
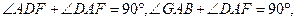
∴
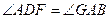 .……………………………………………………………………5分
.……………………………………………………………………5分∵四边形
 是正方形,∴AD=AB,
是正方形,∴AD=AB, 在
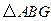 与
与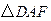 中,
中,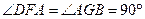 ,
,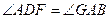 ,AD=AB,
,AD=AB,∴
 (AAS). ………………………………………………………6分
(AAS). ………………………………………………………6分②如果是在AE上截取AG=DF,证明如下:
∵
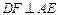 ,AD⊥AE,
,AD⊥AE,∴
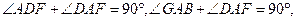
∴
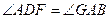 .……………………………………………………………………4分
.……………………………………………………………………4分∵四边形
 是正方形,∴AD=AB, …
是正方形,∴AD=AB, … …………………………………………5分
…………………………………………5分在
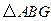 与
与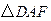 中,AG=DF,
中,AG=DF,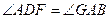 ,AD=AB,
,AD=AB,∴
 (SAS). ………………………………………………………6分
(SAS). ………………………………………………………6分③如果作
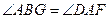 交AE于点G,证明如下:
交AE于点G,证明如下:∵
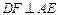 ,AD⊥AE,
,AD⊥AE,∴
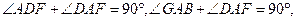
∴
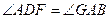 .……………………………………………………………………4分
.……………………………………………………………………4分∵四边形
 是正方形,∴AD=AB, ……………………………………………5分
是正方形,∴AD=AB, ……………………………………………5分在
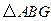 与
与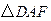 中,
中,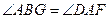 , AD=AB,
, AD=AB,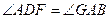
∴
 (ASA). ………………………………………………………6分
(ASA). ………………………………………………………6分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 ,AF=DC,
,AF=DC, 边形ABDE是平行四边形。
边形ABDE是平行四边形。
 状并证明;
状并证明;
 ,求三角形DBF的面积.
,求三角形DBF的面积. 
 =
= ,求证:
,求证: .
.


