题目内容
【题目】如图,平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在一次函数
在一次函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(2)求由直线![]() ,(1)中的直线
,(1)中的直线![]() 以及
以及![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
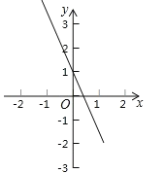
【答案】(1)![]() ; (2)
; (2)![]()
【解析】
(1)先求出A点坐标,再根据关于x轴对称的点的坐标特点得出B点坐标,代入一次函数y=![]() x+b求出b的值即可得出其解析式,画出该函数图象即可;
x+b求出b的值即可得出其解析式,画出该函数图象即可;
(2)设两个一次函数图象的交点为点C,联立两函数的解析式得出C点坐标,利用三角形的面积公式即可得出结论.
(1)∵把x=0代入y=-2x+1,得y=1,
∴点A坐标为(0,1),
∴点B坐标为(0,-1),
∵点B在一次函数y=![]() x+b的图象上,
x+b的图象上,
∴-1=![]() ×0+b,
×0+b,
∴b=-1;
(2)如图:

设两个一次函数图象的交点为点C,
∵ ,解得
,解得 ,
,
∴点C坐标为(![]() ,-
,-![]() ),
),
∴S△ABC=![]() ×2×
×2×![]() =
=![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目