题目内容
【题目】已知:P(4,1)为平面直角坐标系中的一点,点A(a,0),点B(0,a)(其中a>0)分别是坐标轴上的动点,若△PAB的面积为3,试求点A的坐标.
【答案】(2,0)或(3,0)
【解析】
过点P作PC⊥x轴于C,作PD⊥y轴于D,可得四边形OCPD是矩形,再分点C在点A的左边和右边两种情况,表示出AC、BD,再利用梯形的面积和三角形的面积表示出△ABP的面积,然后计算即可得解.
过点P作PC⊥x轴于C,作PD⊥y轴于D,则四边形OCPD是矩形,如图1,
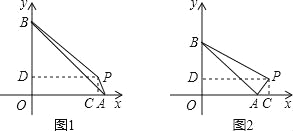
点C在点A的左边时,a>4,
∵P(4,1),点A(a,0),点B(0,a),
∴AC=a﹣4,BD=a﹣1,
△PAB的面积=![]() ×4×(a﹣1)+
×4×(a﹣1)+![]() ×(a﹣4)×1+1×4﹣
×(a﹣4)×1+1×4﹣![]() ×a2=3,
×a2=3,
整理得,a2﹣5a+6=0,
解得a1=2(舍去),a2=3(舍去),
如图2,点C在点A的右边时,a<4,
∵P(4,1),点A(a,0),点B(0,a),
∴AC=4﹣a,BD=a﹣1,
△PAB的面积=![]() ×4×(a﹣1)+4×1﹣
×4×(a﹣1)+4×1﹣![]() ×(4﹣a)×1﹣
×(4﹣a)×1﹣![]() ×a2=3,
×a2=3,
整理得,a2﹣5a+6=0,
解得a1=2,a2=3,
∴点A的坐标为(2,0)或(3,0),
综上所述,若△PAB的面积为3,则点A的坐标为(2,0)或(3,0).

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
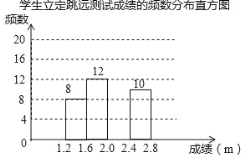
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有850名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?