Question

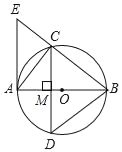
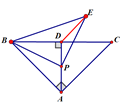
【题目】在Rt△ABC中，∠BAC=90，AB=AC，AD⊥BC于点D，P是线段AD上的一个动点，以点P为直角的顶点，向上作等腰直角三角形PBE，连接DE，若在点P的运动过程中，DE的最小值为3，则AD的长为____．

Answer 1

【答案】

【解析】

当DE⊥CE时，DE的有最小值，根据等腰直角三角形的性质和相似三角形的性质即可得到结论．

当DE⊥CE时，DE的有最小值．

连接CE．∵△BAC和△EBP是等腰直角三角形，∴∠EBC+∠CBP=∠CBP+∠PBA=45°，BC=BA，BE=BP，∴∠EBC=∠PBA，，∴△EBC∽△PBA，∴∠ECB=∠PAB．

∵△BAC是等腰直角三角形，AD⊥BC，∴∠PAB=45°，BD=DC=AD，∴∠ECD=45°．

∵∠DEC=90°，∴△DEC是等腰直角三角形，∴DC=DE=，∴AD=．

故答案为：．