题目内容
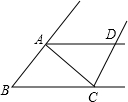
 如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为
如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为
- A.40°
- B.80°
- C.120°
- D.不能确定
B
分析:由△ABC≌△ADE,得∠BAC=∠DAE,则∠BAD=∠CAE,再由∠BAC=∠BAE-∠CAE,即可得出答案.
解答:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠BAC=∠BAE-∠CAE=120°-40°=80°.
故选B.
点评:本题考查了全等三角形的性质,解题的关键是找到两全等三角形的对应角.
分析:由△ABC≌△ADE,得∠BAC=∠DAE,则∠BAD=∠CAE,再由∠BAC=∠BAE-∠CAE,即可得出答案.
解答:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠BAC=∠BAE-∠CAE=120°-40°=80°.
故选B.
点评:本题考查了全等三角形的性质,解题的关键是找到两全等三角形的对应角.

练习册系列答案
相关题目
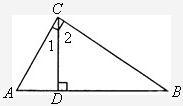
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
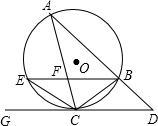
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.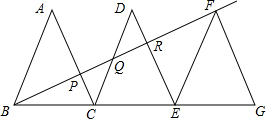 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且