题目内容
如图,网格中每个小正方形的边长均为1.在AB的左侧,分别以△ABC的三边为直径作三个半圆围成图中的阴影部分.(1)图中△ABC是什么特殊三角形?
(2)求图中阴影部分的面积;
(3)作出阴影部分关于AB所在直线的对称图形.

【答案】分析:(1)根据轴对称的知识可得,△ABC是等腰直角三角形;
(2)先求以AC,BC,AB为直径的半圆面积分别为S1,S2,S3,再求S阴影=S1+S2+S△ABC-S3即可;
(3)以AB为对称轴,作图即可.
解答:解:(1)∵四边形ADCE时正方形,
∴∠DAC=45°,
同理∠CBA=45°,
∴△ABC是等腰直角三角形;(2分)
(2)设以AC,BC,AB为直径的半圆面积分别为S1,S2,S3;
解法1:在等腰直角三角形ABC中,
∵AB=8,由勾股定理,可得AC=BC=4 .
.
∴S阴影=S1+S2+S△ABC-S3(3分)
= π(2
π(2 )2+
)2+ π(2
π(2 )2+
)2+ ×(4
×(4 )2-
)2- π×42,
π×42,
=16.(5分)
解法2:S阴影=S1+S2+S△ABC-S3(3分)
= π(
π( )2+
)2+ π(
π( )2+S△ABC-
)2+S△ABC- π(
π( )2,
)2,
= π(AC2+BC2-AB2)+S△ABC.(4分)
π(AC2+BC2-AB2)+S△ABC.(4分)
在Rt△ABC中,由勾股定理知,AC2+BC2=AB2,
∴S阴影=S△ABC= ×8×4=16.(5分)
×8×4=16.(5分)
(3)作图正确(如右图).(8分)
点评:本小题主要考查勾股定理、轴对称图形、中心对称图形的知识,考查动手操作、面积的计算及审美能力.
(2)先求以AC,BC,AB为直径的半圆面积分别为S1,S2,S3,再求S阴影=S1+S2+S△ABC-S3即可;
(3)以AB为对称轴,作图即可.
解答:解:(1)∵四边形ADCE时正方形,
∴∠DAC=45°,
同理∠CBA=45°,
∴△ABC是等腰直角三角形;(2分)
(2)设以AC,BC,AB为直径的半圆面积分别为S1,S2,S3;

解法1:在等腰直角三角形ABC中,
∵AB=8,由勾股定理,可得AC=BC=4
 .
.∴S阴影=S1+S2+S△ABC-S3(3分)
=
 π(2
π(2 )2+
)2+ π(2
π(2 )2+
)2+ ×(4
×(4 )2-
)2- π×42,
π×42,=16.(5分)
解法2:S阴影=S1+S2+S△ABC-S3(3分)
=
 π(
π( )2+
)2+ π(
π( )2+S△ABC-
)2+S△ABC- π(
π( )2,
)2,=
 π(AC2+BC2-AB2)+S△ABC.(4分)
π(AC2+BC2-AB2)+S△ABC.(4分)在Rt△ABC中,由勾股定理知,AC2+BC2=AB2,

∴S阴影=S△ABC=
 ×8×4=16.(5分)
×8×4=16.(5分)(3)作图正确(如右图).(8分)
点评:本小题主要考查勾股定理、轴对称图形、中心对称图形的知识,考查动手操作、面积的计算及审美能力.

练习册系列答案
相关题目
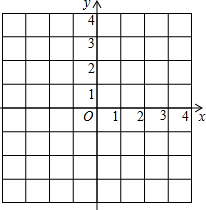 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.
C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.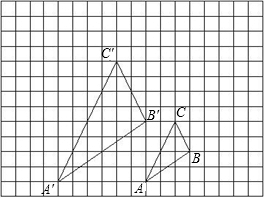 C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.
C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上. 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: