题目内容
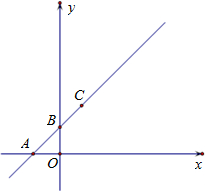
如图,直线y=hx+d与x轴和y轴分别相交于点A(-1,0),B(0,1),与双曲线y=| t |
| x |
 hx+d、双曲线y=
hx+d、双曲线y=| t |
| x |
(1)确定t的值;
(2)确定m,n,k的值;
(3)若无论a,b,c取何值,抛物线y=ax2+bx+c都不经过点P,请确定P的坐标.
分析:(1)可设C点的坐标为(x1,x2),那么矩形的面积应该是x1y1=t;可用C点坐标表示出以AC为斜边、∠CAO为内角的直角三角形的面积,联立两式即可求出C点坐标及t的值;
(2)将顶点B以及点C的坐标代入抛物线y=mx2+nx+k中,即可求出待定系数的值;
(3)在(1)(2)中已经求得了双曲线及直线的解析式,联立两式即可求出点C、D的坐标,将点D的坐标代入抛物线y=ax2+bx+c中,可求出a、c以及a、b的关系式,可用a替换掉b、c,然后根据抛物线y=mx2+nx+k的解析式来设P点的坐标,若P点不在抛物线y=ax2+bx+c上,那么将P点坐标代入上面的解析式后左右两边不相等,可据此来求P点的坐标.
(2)将顶点B以及点C的坐标代入抛物线y=mx2+nx+k中,即可求出待定系数的值;
(3)在(1)(2)中已经求得了双曲线及直线的解析式,联立两式即可求出点C、D的坐标,将点D的坐标代入抛物线y=ax2+bx+c中,可求出a、c以及a、b的关系式,可用a替换掉b、c,然后根据抛物线y=mx2+nx+k的解析式来设P点的坐标,若P点不在抛物线y=ax2+bx+c上,那么将P点坐标代入上面的解析式后左右两边不相等,可据此来求P点的坐标.
解答:解:(1)直线过点A,B,则0=-h+d和1=d,即y=x+1. (1分)
双曲线y=
经过点C(x1,y1),x1y1=t.
以AC为斜边,∠CAO为内角的直角三角形的面积为
×y1×(1+x1);
以CO为对角线的矩形面积为x1y1.
×y1×(1+x1)=x1y1,
因为x1,y1都不等于0,
故得x1=1,
所以y1=2.
故有,2=
,
故t=2×1=2,即t=2. (2分)
(2)∵B是抛物线y=mx2+nx+k的顶点,
∴有-
=0,-
=1,
得到n=0,k=1. (3分)
∵C是抛物线y=mx2+nx+k上的点,
∴有2=m×12+1,得m=1. (4分)
故m=1,n=0,k=1.
(3)设点P的横坐标为p,则纵坐标为p2+1.
∵抛物线y=ax2+bx+c经过两个不同的点C,D,
其中求得D点坐标为(-2,-1). (5分)
解法一:
故2=a+b+c,
-1=4a-2b+c.
解之得,b=a+1,c=1-2a. (6分)
(说明:如用b表示a,c,或用c表示a,b,均可,后续参照得分)
∴y=ax2+(a+1)x+(1-2a)
于是:p2+1≠ap2+(a+1)p+(1-2a) (7分)
变形,得p2-p≠(p2+p-2)a,
∴无论a取什么值都有p2-p≠(p2+p-2)a. (8分)
(或者,令p2-p=(p2+p-2)a (7分)
∵抛物线y=ax2+bx+c不经过P点,
∴此方程无解,或有解但不合题意(8分)
故∵a≠0,
∴①
解之p=0,p=1,并且p≠1,p≠-2.得p=0 (9分)
∴符合题意的P点为(0,1)(10分)
②
,
解之p=1,p=-2,并且p≠0,p≠1.
得p=-2. (11分)
符合题意的P点为(-2,5). (12分)
∴符合题意的P点有两个(0,1)和(-2,5).
解法二:则有(a-1)p2+(a+1)p-2a=0 (7分)
即〔(a-1)p+2a〕(p-1)=0
有p-1=0时,得p=1,
即C点(1,2)在y=ax2+bx+c上. (8分)
或(a-1)p+2a=0,即(p+2)a=p
当p=0时a=0与a≠0矛盾(9分)
得点P(0,1)(10分)
或者p=-2时,无解(11分)
得点P(-2,5)(12分)
故对任意a,b,c,抛物线y=ax2+bx+c都不经过(0,1)和(-2,5)
解法三:如图,抛物线y=ax2+bx+c不经过直线CD上除C,D外的其他点;
(只经过直线CD上的C,D点). (6分)
由
(7分)
解得交点为C(1,2),B(0,1);
故符合题意的点P为(0,1). (8分)
抛物线y=ax2+bx+c不经过直线x=-2上除D外的其他点. (9分)
由
(10分)
解得交点P为(-2,5).(11分)
抛物线y=ax2+bx+c不经过直线x=1上除C外的其他点,
而
解得交点为C(1,2). (12分)
故符合条件的点P为(0,1)或(-2,5).
(说明:1.仅由图形看出一个点的坐标给(1分),二个看出来给(2分).2,解题过程叙述基本清楚即可.)
双曲线y=
| t |
| x |
以AC为斜边,∠CAO为内角的直角三角形的面积为
| 1 |
| 2 |
以CO为对角线的矩形面积为x1y1.
| 1 |
| 2 |
因为x1,y1都不等于0,
故得x1=1,
所以y1=2.
故有,2=
| t |
| 1 |
故t=2×1=2,即t=2. (2分)
(2)∵B是抛物线y=mx2+nx+k的顶点,
∴有-
| n |
| 2m |
| n2-4mk |
| 4m |
得到n=0,k=1. (3分)
∵C是抛物线y=mx2+nx+k上的点,

∴有2=m×12+1,得m=1. (4分)
故m=1,n=0,k=1.
(3)设点P的横坐标为p,则纵坐标为p2+1.
∵抛物线y=ax2+bx+c经过两个不同的点C,D,
其中求得D点坐标为(-2,-1). (5分)
解法一:
故2=a+b+c,
-1=4a-2b+c.
解之得,b=a+1,c=1-2a. (6分)
(说明:如用b表示a,c,或用c表示a,b,均可,后续参照得分)
∴y=ax2+(a+1)x+(1-2a)
于是:p2+1≠ap2+(a+1)p+(1-2a) (7分)
变形,得p2-p≠(p2+p-2)a,
∴无论a取什么值都有p2-p≠(p2+p-2)a. (8分)
(或者,令p2-p=(p2+p-2)a (7分)
∵抛物线y=ax2+bx+c不经过P点,
∴此方程无解,或有解但不合题意(8分)
故∵a≠0,
∴①
|
解之p=0,p=1,并且p≠1,p≠-2.得p=0 (9分)
∴符合题意的P点为(0,1)(10分)
②
|
解之p=1,p=-2,并且p≠0,p≠1.
得p=-2. (11分)
符合题意的P点为(-2,5). (12分)
∴符合题意的P点有两个(0,1)和(-2,5).
解法二:则有(a-1)p2+(a+1)p-2a=0 (7分)
即〔(a-1)p+2a〕(p-1)=0
有p-1=0时,得p=1,
即C点(1,2)在y=ax2+bx+c上. (8分)
或(a-1)p+2a=0,即(p+2)a=p
当p=0时a=0与a≠0矛盾(9分)
得点P(0,1)(10分)
或者p=-2时,无解(11分)
得点P(-2,5)(12分)
故对任意a,b,c,抛物线y=ax2+bx+c都不经过(0,1)和(-2,5)
解法三:如图,抛物线y=ax2+bx+c不经过直线CD上除C,D外的其他点;
(只经过直线CD上的C,D点). (6分)
由
|
解得交点为C(1,2),B(0,1);
故符合题意的点P为(0,1). (8分)
抛物线y=ax2+bx+c不经过直线x=-2上除D外的其他点. (9分)
由
|
解得交点P为(-2,5).(11分)
抛物线y=ax2+bx+c不经过直线x=1上除C外的其他点,
而
|
故符合条件的点P为(0,1)或(-2,5).
(说明:1.仅由图形看出一个点的坐标给(1分),二个看出来给(2分).2,解题过程叙述基本清楚即可.)
点评:此题是一次函数、二次函数的综合题,主要考查了函数解析式的确定、图形面积的求法、函数图象交点等知识,综合性强,难度很大.

练习册系列答案
相关题目
 在第一象限相交于点C;以AC为斜边、∠CAO为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=mx2+nx+k上;直线y=hx+d、双曲线y=
在第一象限相交于点C;以AC为斜边、∠CAO为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=mx2+nx+k上;直线y=hx+d、双曲线y= 和抛物线y=ax2+bx+c同时经过两个不同的点C,D.
和抛物线y=ax2+bx+c同时经过两个不同的点C,D.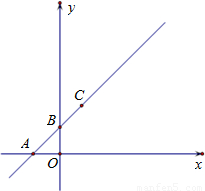
 在第一象限相交于点C;以AC为斜边、
在第一象限相交于点C;以AC为斜边、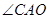 为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=
为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y= 上;直线y=hx+d、双曲线y=
上;直线y=hx+d、双曲线y= 同时经过两个不同的点C,D
同时经过两个不同的点C,D
 在第一象限相交于点C;以AC为斜边、
在第一象限相交于点C;以AC为斜边、 为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=
为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y= 上;直线y=hx+d、双曲线y=
上;直线y=hx+d、双曲线y=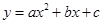 同时经过两个不同的点C,D
同时经过两个不同的点C,D