题目内容
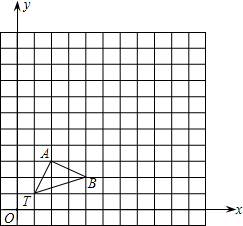 如图,在正方形网格中,△TAB的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
如图,在正方形网格中,△TAB的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).(1)以点T(1,1)为位似中心,在位似中心的同侧将△TAB放大为原来的3倍,放大后点A、B的对应点分别为A′、B′,画出△TA′B′:
(2)写出点A′、B′的坐标:A′(
4
4
,7
7
)、B′(10
10
,4
4
);(3)在(1)中,若C(a,b)为线段AB上任一点,则变化后点C的对应点C′的坐标为(
3a-2
3a-2
,3b-2
3b-2
).分析:(1)根据题目的叙述,在位似中心的同侧将△TAB放大为原来的3倍,得到对应点坐标,正确地作出图形即可,
(2)根据图象确定各点的坐标即可.
(3)根据(2)中变换的规律,即可写出变化后点C的对应点C′的坐标.
(2)根据图象确定各点的坐标即可.
(3)根据(2)中变换的规律,即可写出变化后点C的对应点C′的坐标.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)点A′,B′的坐标分别为:A′(4,7),B′(10,4);
故答案为:4,7;10,4;
(3)变化后点C的对应点C′的坐标为:C′(3a-2,3b-2)
故答案为:3a-2,3b-2.
 解:(1)如图所示:
解:(1)如图所示:(2)点A′,B′的坐标分别为:A′(4,7),B′(10,4);
故答案为:4,7;10,4;
(3)变化后点C的对应点C′的坐标为:C′(3a-2,3b-2)
故答案为:3a-2,3b-2.
点评:本题考查位似变换作图的问题,正确理解位似变换的定义,会进行位似变换的作图是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
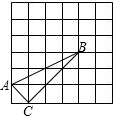 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
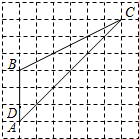 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
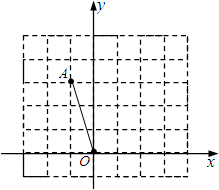 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).