题目内容
 如图,弧
如图,弧 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是
上任意一点,若AC=5,则四边形ACBP周长的最大值是
- A.15
- B.20
- C.15+

- D.15+
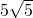
C
分析:因为P在半径为5的圆周上,若使四边形周长最大,只要AP最长即可(因为其余三边长为定值5).
解答:由于AC和BC值固定,点P在弧AD上,而B是圆心,所以PB的长也是定值,
因此,只要AP的长为最大值,
∴当P的运动到D点时,AP最长为5 ,所以周长为5×3+5
,所以周长为5×3+5 =15+5
=15+5 .
.
故选C.
点评:本题考查的是勾股定理和最值.本题容易出现错误的地方是对点P的运动状态不清楚,无法判断什么时候会使周长成为最大值.
分析:因为P在半径为5的圆周上,若使四边形周长最大,只要AP最长即可(因为其余三边长为定值5).
解答:由于AC和BC值固定,点P在弧AD上,而B是圆心,所以PB的长也是定值,
因此,只要AP的长为最大值,
∴当P的运动到D点时,AP最长为5
 ,所以周长为5×3+5
,所以周长为5×3+5 =15+5
=15+5 .
.故选C.
点评:本题考查的是勾股定理和最值.本题容易出现错误的地方是对点P的运动状态不清楚,无法判断什么时候会使周长成为最大值.

练习册系列答案
相关题目
 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
上任意一点,若AC=5,则四边形ACBP周长的最大值是( )


 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
上任意一点,若AC=5,则四边形ACBP周长的最大值是( )


 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
上任意一点,若AC=5,则四边形ACBP周长的最大值是( )


 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
上任意一点,若AC=5,则四边形ACBP周长的最大值是( )


 是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧
是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧 上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
上任意一点,若AC=5,则四边形ACBP周长的最大值是( )

