题目内容
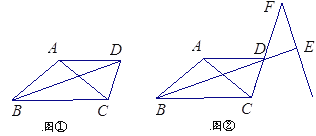
【题目】如本题图①,在△ABC中,已知![]() . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求![]() 的大小;
的大小;
(2)在线段![]() 的延长线上取一点
的延长线上取一点![]() ,以
,以![]() 为角的一边作
为角的一边作![]() ,另一边交BD延长线于点E, 若
,另一边交BD延长线于点E, 若![]() (如本题图②所示),试求
(如本题图②所示),试求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)根据角平分线的性质得出∠1和∠2的度数。根据平行线得出∠1=∠3,∠CAD=∠ACB=α,即AB=AD=AC,从而得出∠ACD的度数;(2)利用三角形相似的性质来得出三角形面积之间的关系,然后得出答案.
试题解析:(1) ∵![]() ,
, ![]() 平分
平分![]() ,
,

∴![]() ,
, ![]() . ∵
. ∵![]() ∥
∥![]() ,∴
,∴![]() , ∴
, ∴![]() .∴
.∴![]() .
.
∴![]() .
. ![]()
![]() .又 ∵
.又 ∵![]() ∥
∥![]() ,
,
![]() ,
, ![]()
(2过![]() 作
作![]() 于点
于点![]() ,
,

则![]() .
. ![]() . ∵
. ∵![]() ∥
∥![]() ,
, ![]()
即: ![]() , 由
, 由![]() ,
, ![]()
![]()
得: ![]() .
.
![]() .
. ![]() .又
.又![]() ,
,
∴△![]() ∽△
∽△![]() . ∵
. ∵![]() ,
, ![]() ,
,
![]() , ∵
, ∵![]() ∥
∥![]() ,∴
,∴![]() .
. ![]()
![]() .
.

练习册系列答案
相关题目
【题目】某班40名学生的某次数学成绩如下表:
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
人数(人) | 2 | m | 10 | n | 4 | 2 |
(1)若这班的数学成绩为69分,求m和n的值.
(2)若该班40名学生成绩的众数为X,中位数为Y.则(X-Y)2的值.