题目内容
写出函数y=3（x-1）2与y=x2-1所具有的一个共同性质________．
开口向上
分析：两函数解析式可看作抛物线解析式的顶点式，a＞0，开口向上，顶点坐标分别为（1，0），（0，-1），故对称轴，增减性，最大（小）值不同，与x轴（y轴）的交点也不同．
解答：∵两个二次函数解析式中，二次项系数a=3和a=1，都为正数，
∴两抛物线都开口向上．
点评：比较二次函数的性质，主要是比较抛物线的开口方向，顶点坐标，与x轴（y轴）的交点情况．
分析：两函数解析式可看作抛物线解析式的顶点式，a＞0，开口向上，顶点坐标分别为（1，0），（0，-1），故对称轴，增减性，最大（小）值不同，与x轴（y轴）的交点也不同．
解答：∵两个二次函数解析式中，二次项系数a=3和a=1，都为正数，
∴两抛物线都开口向上．
点评：比较二次函数的性质，主要是比较抛物线的开口方向，顶点坐标，与x轴（y轴）的交点情况．
练习册系列答案
初中学业考试导与练系列答案
相关题目
，求y与x之间的函数解析式，并写出函数自变量x的取值范围．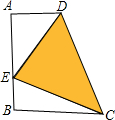
如图，已知在梯形ABCD中，AD∥BC，∠A=90°，AD=2，AB=BC=4，在线段AB上有一动点E，设BE=x，△DEC的面积 S△DEC=y，问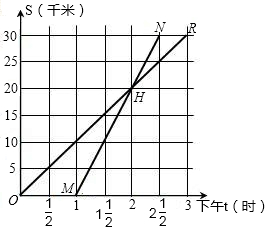
蓄电池的电压为定值，使用此电源时，电流I（A）与电阻（Ω）之间的函数关系图象如图所示，①通过图象你能得到什么信息（至少写出一条）？②写出函数关系式；③当电阻R=8Ω时，电流是多少？