题目内容
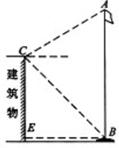
 如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则求旗杆顶点A离地面的高度(结果保留根号).
如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则求旗杆顶点A离地面的高度(结果保留根号).
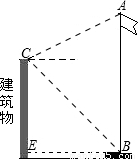
【答案】分析:作CH⊥AB于H,在Rt△ACH中求出AH,在Rt△CHB中求出BH,即可得出答案.
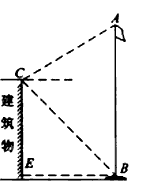
解答:解:如图,作CH⊥AB于H,
在Rt△ACH中,∵∠ACH=30°,tan30°=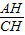 ,
,
∴AH=CH•tan30°=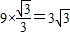 米,
米,
在Rt△CHB中,
∵∠HCB=45°,tan45°=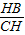 ,
,
∴BH=CH•tan45°=9米,
答:旗杆顶点A离地面的高度为 米.
米.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.
解答:解:如图,作CH⊥AB于H,

在Rt△ACH中,∵∠ACH=30°,tan30°=
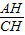 ,
,∴AH=CH•tan30°=
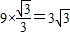 米,
米,在Rt△CHB中,
∵∠HCB=45°,tan45°=
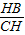 ,
,∴BH=CH•tan45°=9米,
答:旗杆顶点A离地面的高度为
 米.
米.点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.

练习册系列答案
相关题目
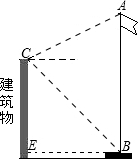 (2013•大港区一模)如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则求旗杆顶点A离地面的高度(结果保留根号).
(2013•大港区一模)如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则求旗杆顶点A离地面的高度(结果保留根号). ,旗杆底部
,旗杆底部 点的俯角为
点的俯角为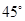 .若旗杆底部
.若旗杆底部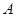 离地面的高度为---米(结果保留根号)。
离地面的高度为---米(结果保留根号)。