题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
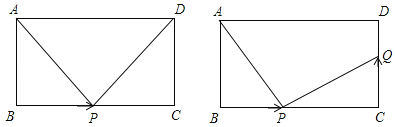
①若点![]() 在线段
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

【答案】(1)、CQ=2.4;(2)、![]() ,(0<x<8);
,(0<x<8);![]() (x≥8)
(x≥8)
【解析】
试题分析:(1)、根据∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC得出∠BAP=∠CQP,然后得到△CPQ∽△BAP,根据相似比得出CQ的长度;(2)、若点P在线段CB上,根据第一题的相似比得出函数解析式;若点P在线段CB的延长线上,根据同样的方法证明△QCP∽△PBA,然后根据相似比得出函数解析式.
试题解析:(1)、∵∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC,∴∠BAP=∠CQP.又∵AB=AC,∴∠B=∠C.
∴△CPQ∽△BAP.∴![]() .∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴
.∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴![]() ,
,![]() .
.
(2)、若点P在线段CB上,由(1)知![]() ,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
又∵CQ=y,AB=5,∴![]() ,即
,即![]() .故所求的函数关系式为
.故所求的函数关系式为![]() ,(0<x<8).
,(0<x<8).
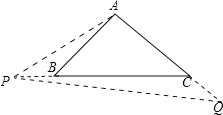
若点P在线段CB的延长线上,如图.∵∠APQ=∠APB+∠CPQ,∠ABC=∠APB+∠PAB,∠APQ=∠ABC,
∴∠CPQ=∠PAB.又∵∠ABP=180°﹣∠ABC,∠PCQ=180°﹣∠ACB,∠ABC=∠ACB,
∴∠ABP=∠PCQ.∴△QCP∽△PBA.∴![]() .∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
.∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
∴![]() ,即
,即![]() (x≥8)
(x≥8)

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元.