Question

求证：菱形四条边的中点在以对角线交点为圆心的同一个圆上．

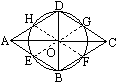
已知：如图所示，菱形ABCD的对角线AC和BD相交于点O，而点E，F，G，H分别是AB，BC，CD，DA的中点．求证：E，F，G，H在以点O为圆心的同一个圆上．

Answer 1

答案：
解析：

证明：连结OE，OF，OG，OH，因为四边形ABCD是菱形，所以AC⊥BD，AB＝BC＝CD＝DA．而E，F，G，H分别是AB，BC，CD，DA的中点，所以OE＝OF＝OG＝OH＝AB，所以E，F，G，H四个点在以O为圆心，以AB为半径的圆上． 　　解题指导：要证明E，F，G，H四个点在以O为圆心的同一个圆上，只需证明EO＝FO＝GO＝HO，因为E，F，G，H是菱形各边的中点，又因为菱形的对角线互相垂直，根据直角三角形斜边中线等于斜边的一半，可得EO＝FO＝GO＝HO＝AB，命题得证．