题目内容
如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，4），C（n，-6），A（5，0），则AD•BC=________．
50
分析：由B，C及A得到坐标，确定出BE，CF及OA的长，三角形ABC面积=三角形AOB面积+三角形AOC面积，三角形ABC面积=AD与BC乘积的一半，两者相等即可求出AD与BC的乘积．
解答：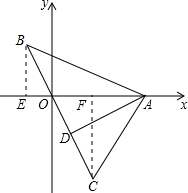
解：∵B（m，4），C（n，-6），A（5，0），
∴BE=4，CF=6，OA=5，
∵S△ABC=S△AOB+S△AOC=
OA•BE+OA•CF=10+15=25，
S△ABC=AD•BC，
∴AD•BC=25，
则AD•BC=50．
故答案为：50．
点评：此题考查了一次函数综合题，涉及的知识有：坐标与图形性质，三角形的面积求法，求出三角形ABC的面积是解本题的关键．
分析：由B，C及A得到坐标，确定出BE，CF及OA的长，三角形ABC面积=三角形AOB面积+三角形AOC面积，三角形ABC面积=AD与BC乘积的一半，两者相等即可求出AD与BC的乘积．
解答：
解：∵B（m，4），C（n，-6），A（5，0），∴BE=4，CF=6，OA=5，
∵S△ABC=S△AOB+S△AOC=
OA•BE+OA•CF=10+15=25，S△ABC=
AD•BC，∴
AD•BC=25，则AD•BC=50．
故答案为：50．
点评：此题考查了一次函数综合题，涉及的知识有：坐标与图形性质，三角形的面积求法，求出三角形ABC的面积是解本题的关键．
练习册系列答案
相关题目
