题目内容
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
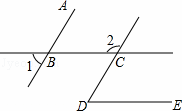
考点:
平行线的判定.
分析:
由于∠1=47°,∠2=133°,则∠ABC+∠2=180°,根据平行线的判定方法得到AB∥CD;然后利用平角的定义计算出∠BCD=180°﹣133°=47°,
则∠BCD=∠D,根据平行线的判定即可得到BC∥DE.
解答:
解:BC∥DE,AB∥CD.理由如下:
∵∠1=47°,∠2=133°,
而∠ABC=∠1=47°,
∴∠ABC+∠2=180°,
∴AB∥CD;
∵∠2=133°,
∴∠BCD=180°﹣133°=47°,
而∠D=47°,
∴∠BCD=∠D,
∴BC∥DE.
点评:
本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
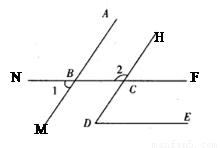
 如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?