题目内容
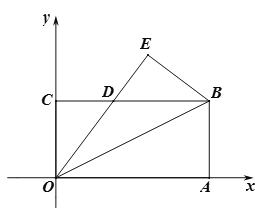
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】(1)证明见解析;(2)点E的坐标为![]() ;(3)F点坐标为
;(3)F点坐标为![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据折叠的性质,得到△OBE≌△OBA,由此得到∠EOB=∠AOB,然后根据矩形的性质和平行线的性质得到OD=BD,即△OBD是等腰三角形;
(2)过点E作![]() 轴于F交BC于G,设CD的长为
轴于F交BC于G,设CD的长为![]() ,则
,则![]() ,由(1)值OD=8-x,然后根据勾股定理求出CD、OB、BD的长,再根据AAS证得△OCD≌△BED,得到
,由(1)值OD=8-x,然后根据勾股定理求出CD、OB、BD的长,再根据AAS证得△OCD≌△BED,得到![]() ,最后根据三角形的面积求出EG的长,进而利用矩形的性质和勾股定理求出E点的坐标;
,最后根据三角形的面积求出EG的长,进而利用矩形的性质和勾股定理求出E点的坐标;
(3)根据平行四边形的判定与性质,分类讨论F点的坐标即可.
(1)∵![]() 是由
是由![]() 折叠所得
折叠所得
∴![]() ≌
≌![]() .,
.,
∴![]() ,
,
又∵四边形OABC是矩形
∴![]() .,
.,
∴![]()
∴![]() ,
,
∴![]() 为等腰三角形;
为等腰三角形;
(2)过点E作![]() 轴于F交BC于G
轴于F交BC于G
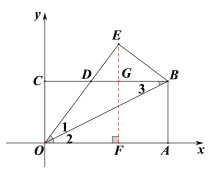
设CD的长为![]() ,则
,则![]()
由(1)知![]()
∵四边形OABC是矩形
∴![]()
∴在![]() 中
中![]()
即![]()
解得![]()
即![]()
由(1)知![]() ≌
≌![]()
∴![]()
∴![]()
∴ 在△OCD和△BED中
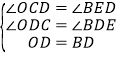
∴△OCD≌△BED
∴![]()
∵![]() 轴
轴
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
∴![]() .
.
∴在![]() 中
中![]()
∵![]()
∴四边形OFGC是矩形
∴![]()
![]() .
.
∴点E的坐标为![]() ;
;
(3)![]()
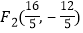
![]() .
.

练习册系列答案
相关题目