题目内容
已知四边形ABCD,连接AC、BD交于点O,且满足条件:AB+DC=AD+BC,AB2+AD2=BC2+DC2,
(1)若AB=AD,求证:∠BAC=∠BCA;
(2)若AB>AD,当OD绕点O逆时针旋转180°时,点D能否落在线段OB上,并说明理由.
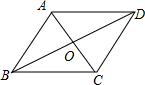 (1)证明:∵AB+DC=AD+BC,AB=AD,
(1)证明:∵AB+DC=AD+BC,AB=AD,∴DC=BC,
∵AB2+AD2=BC2+DC2,
∴AB=AD=BC=DC,
∴∠BAC=∠BCA;
 (2)当OD绕点O逆时针旋转180°时,点D能落在线段OB上.
(2)当OD绕点O逆时针旋转180°时,点D能落在线段OB上.∵AB2+AD2=BC2+DC2,
∴AB2-DC2=BC2-AD2,
∴(AB+DC)(AB-DC)=(AD+BC)(BC-AD),
∵AB+DC=AD+BC,
∴AB-DC=BC-AD,
∴AB=BC,DC=AD,
∴BD垂直平分AC,且OB>OD,
∴当OD绕点O逆时针旋转180°时,点D能落在线段OB上.
分析:(1)由AB+DC=AD+BC,AB2+AD2=BC2+DC2,AB=AD,可得AB=AD=BC=DC,然后由等边对等角,即可证得∠BAC=∠BCA;
(2)由AB+DC=AD+BC,AB2+AD2=BC2+DC2,可证得AB=BC,DC=AD,又由AB>AD,可得BD垂直平分AC,且OB>OD,即可得当OD绕点O逆时针旋转180°时,点D能落在线段OB上.
点评:此题考查了等腰三角形的性质、线段垂直平分线的性质以及平方差公式的应用.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
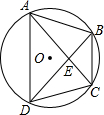 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |
如图,已知四边形ABCD是边长为2的正方形,E是AB的中点,F是BC的中点,AF与DE相交于G,BD和AF相交于H,那么四边形BEGH的面积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
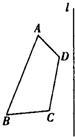 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.