题目内容
如图,分别过反比例函数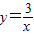 图象上的点P1(1,y1),P2(2,y2),…,Pn(n,Pn)….作x轴的垂线,垂足分别为A1,A2…An …,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,依此类推,则点Bn的纵坐标是 .(结果用含n代数式表示)
图象上的点P1(1,y1),P2(2,y2),…,Pn(n,Pn)….作x轴的垂线,垂足分别为A1,A2…An …,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,依此类推,则点Bn的纵坐标是 .(结果用含n代数式表示)
【答案】分析:根据反比例函数图象上点的坐标特征求得点P1、P2的纵坐标,由平行四边形对边平行且相等的性质求得点B1的纵坐标是y2+y1、B2的纵坐标是y3+y2、B3的纵坐标是y4+y3,据此可以推知点Bn的纵坐标是:yn+1+yn=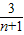 +
+ =
= .
.
解答:解:∵点P1(1,y1),P2(2,y2)在反比例函数 的图象上,
的图象上,
∴y1=3,y2= ;
;
∴P1A1=y1=3;
又∵四边形A1P1B1P2,是平行四边形,
∴P1A1=B1P2=3,P1A1∥B1P2 ,
∴点B1的纵坐标是:y2+y1= +3,即点B1的纵坐标是
+3,即点B1的纵坐标是 ;
;
同理求得,点B2的纵坐标是:y3+y2=1+ =
= ;
;
点B3的纵坐标是:y4+y3= +1=
+1= ;
;
…
点Bn的纵坐标是:yn+1+yn= +
+ =
= ;
;
故答案是: .
.
点评:本题考查了平行四边形的性质、反比例函数图象上点的坐标特征、反比例函数的图象.解答此题的关键是根据平行四边形的对边平行且相等的性质求得点Bn的纵坐标yn+1+yn.
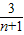 +
+ =
= .
.解答:解:∵点P1(1,y1),P2(2,y2)在反比例函数
 的图象上,
的图象上,∴y1=3,y2=
 ;
;∴P1A1=y1=3;
又∵四边形A1P1B1P2,是平行四边形,
∴P1A1=B1P2=3,P1A1∥B1P2 ,
∴点B1的纵坐标是:y2+y1=
 +3,即点B1的纵坐标是
+3,即点B1的纵坐标是 ;
;同理求得,点B2的纵坐标是:y3+y2=1+
 =
= ;
;点B3的纵坐标是:y4+y3=
 +1=
+1= ;
;…
点Bn的纵坐标是:yn+1+yn=
 +
+ =
= ;
;故答案是:
 .
.点评:本题考查了平行四边形的性质、反比例函数图象上点的坐标特征、反比例函数的图象.解答此题的关键是根据平行四边形的对边平行且相等的性质求得点Bn的纵坐标yn+1+yn.

练习册系列答案
相关题目
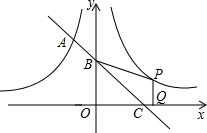 如图,一次函数的图象与反比例函数
如图,一次函数的图象与反比例函数
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
 点A在y轴的正半轴上,过点A作直线
点A在y轴的正半轴上,过点A作直线 ,AC:AB=2:3,则k1=( ),k2=( )。
,AC:AB=2:3,则k1=( ),k2=( )。