题目内容
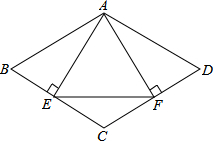 (2013•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是
(2013•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是3
| 3 |
3
.| 3 |
分析:首先利用菱形的性质及等边三角形的判定可得判断出△AEF是等边三角形,再根据三角函数计算出AE=EF的值,再过A作AM⊥EF,再进一步利用三角函数计算出AM的值,即可算出三角形的面积.
解答: 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴AB•AE=AD•AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴AE=2
,
∴EF=AE=2
,
过A作AM⊥EF,
∴AM=AE•cos60°=3,
∴△AEF的面积是:
EF•AM=
×2
×3=3
.
故答案为:3
.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴AB•AE=AD•AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴AE=2
| 3 |
∴EF=AE=2
| 3 |
过A作AM⊥EF,
∴AM=AE•cos60°=3,
∴△AEF的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:3
| 3 |
点评:此题考查菱形的性质,等边三角形的判定及三角函数的运用.关键是掌握菱形的性质,证明△AEF是等边三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
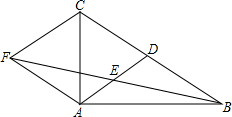 (2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.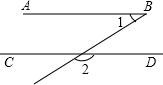 (2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
(2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
 (2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )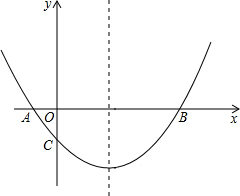 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,