题目内容
(1)已知关于x的方程2x2-3x+m+1=0.①当m<0时,求这个方程的根;
②如果这个方程没有实数根,求m的取值范围.
(2)二次函数的图象经过点(1,0),(0,5),(-1,8),求这个二次函数的解析式,并写出图象顶点的坐标.
(3)某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表所示
| 部门 | 人数 | 每人所创的年利润(万元) |
| A | 1 | 20 |
| B | 1 | 5 |
| C | 2 | 2.5 |
| D | 4 | 2.1 |
| E | 2 | 1.5 |
| F | 2 | 1.5 |
| G | 3 | 1.2 |
①该公司每人所创年利润的平均数是
②该公司每人所创年利润的中位数是
③你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?答:
(4)已知BE:EC=3:1,S△FBE=18,求S△FDA.

分析:(1)根据根的判别式来确定m的取值;
(2)设二次函数的解析式为y=ax2+bx+c(a≠0),把点(1,0),(0,5),(-1,8)代入该方程,用待定系数法求二次函数的解析式;
(3)①平均数=
;
②当一组数据从小到大排列后,最中间的数据为中位数(偶数个数据的最中间两个的平均数);
③应该用中位数来描述该公司每人所创年利润的一般水平;
(4)△FDA∽△FBE,相似三角形的面积比等于相似比.
(2)设二次函数的解析式为y=ax2+bx+c(a≠0),把点(1,0),(0,5),(-1,8)代入该方程,用待定系数法求二次函数的解析式;
(3)①平均数=
| 总利润 |
| 总人数 |
②当一组数据从小到大排列后,最中间的数据为中位数(偶数个数据的最中间两个的平均数);
③应该用中位数来描述该公司每人所创年利润的一般水平;
(4)△FDA∽△FBE,相似三角形的面积比等于相似比.
解答:解:(1)△=(-3)2-4×2(m+1)=1-8m(1分)
①∵m<0,∴1-8m>0
∴x=
;(3分)
②如果方程没有实数根,那么△=1-8m<0(1分)
∴m的取值范围是m>
. (1分)
(2)设二次函数的解析式为y=ax2+bx+c(a≠0)(1分)
根据题意,得:
(2分)
解得
(2分)
∴函数的解析式为y=-x2-4x+5.
∵y=-x2-4x+5=-(x+2)2+9,
∴函数图象的顶点的坐标为(-2,9).(1分)
(3)①15个人每年所创的总利润:20×1+5×1+2.5×2+2.1×4+1.5×2+1.5×2+1.2×3=48,
∴平均数=
=
=3.2;
故该公司每人所创年利润的平均数是3.2万元.
②当一组数据从小到大排列后,最中间的数据为中位数,所以,该公司每人所创年利润的中位数是最中间的数据2.1.
③平均数反映了一组数据的平均大小,常用来一代表数据的总体“平均水平”,而中位数像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”.本题用来来描述该公司每人所创年利润的一般水平,所以答案是:中位数.
(4)∵
=
,∴
=
(1分)
∵四边形ABCD是平行四边形,
∴∠FAD=∠FEB,∠FDA=∠FBE(同位角相等),
又∵∠AFD=∠EFB(对顶角相等),
∴△FDA∽△FBE(AAA),(1分)
∴
=(
)2=(
)2(2分)
∴
=
∴S△FDA=
×S△FBE=
×18=32.(2分)
①∵m<0,∴1-8m>0
∴x=
3±
| ||
| 4 |
②如果方程没有实数根,那么△=1-8m<0(1分)
∴m的取值范围是m>
| 1 |
| 8 |
(2)设二次函数的解析式为y=ax2+bx+c(a≠0)(1分)
根据题意,得:
|
解得
|
∴函数的解析式为y=-x2-4x+5.
∵y=-x2-4x+5=-(x+2)2+9,
∴函数图象的顶点的坐标为(-2,9).(1分)
(3)①15个人每年所创的总利润:20×1+5×1+2.5×2+2.1×4+1.5×2+1.5×2+1.2×3=48,
∴平均数=
| 总利润 |
| 总人数 |
| 48 |
| 15 |
故该公司每人所创年利润的平均数是3.2万元.
②当一组数据从小到大排列后,最中间的数据为中位数,所以,该公司每人所创年利润的中位数是最中间的数据2.1.
③平均数反映了一组数据的平均大小,常用来一代表数据的总体“平均水平”,而中位数像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”.本题用来来描述该公司每人所创年利润的一般水平,所以答案是:中位数.
(4)∵
| BE |
| EC |
| 3 |
| 1 |
| BE |
| BC |
| 3 |
| 4 |
∵四边形ABCD是平行四边形,
∴∠FAD=∠FEB,∠FDA=∠FBE(同位角相等),
又∵∠AFD=∠EFB(对顶角相等),
∴△FDA∽△FBE(AAA),(1分)
∴
| S△FDA |
| S△FBE |
| AD |
| BE |
| 4 |
| 3 |
∴
| S△FDA |
| S△FBE |
| 16 |
| 9 |
∴S△FDA=
| 16 |
| 9 |
| 16 |
| 9 |
点评:(1)一元二次方程根的情况与判别式△的关系:
①△>0?方程有两个不相等的实数根;
②△=0?方程有两个相等的实数根;
③△<0?方程没有实数根.
(2)用待定系数法求二次函数解析式;
(3)分清平均数与中位数:平均数是一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数.
中位数是将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数.
(4)相似三角形的性质:相似三角形的面积比等于相似比.
①△>0?方程有两个不相等的实数根;
②△=0?方程有两个相等的实数根;
③△<0?方程没有实数根.
(2)用待定系数法求二次函数解析式;
(3)分清平均数与中位数:平均数是一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数.
中位数是将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数.
(4)相似三角形的性质:相似三角形的面积比等于相似比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
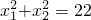 ,求m的值.
,求m的值.