题目内容
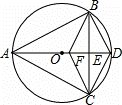
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.

(1)证明:∵AD是直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
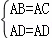 ,
,
∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)四边形BFCD是菱形.
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中
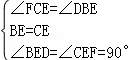 ,
,
∴△BED≌△CEF,
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DE•AE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD= =
=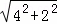 =2
=2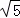 .
.

练习册系列答案
相关题目
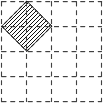
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
|
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
如图是一个螺母的示意图,它的俯视图是( )

|
| A. |
| B. |
| C. |
| D. |
|

 •(m﹣n),其中
•(m﹣n),其中 =2.
=2.








 、
、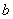 、
、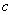 ,且
,且 ,若平行于三角形一边的直线
,若平行于三角形一边的直线 △ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为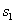 、
、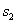 、
、 则
则