题目内容
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.

(1)当OC= 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
(2)当OC> 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。
【答案】
(1)见解析(2)① ②存在,这样的梯形有2个
②存在,这样的梯形有2个
【解析】解:(1)如图①,连接OD,

则 。
。
∵CD=OA=2,OC= ,
,
∴ 。
。
∴ 。
。
∴△OCD是直角三角形,且∠ODC=900。
∴CD为⊙O的切线。
(2)如图②,连接OE,OD,

∵OD=OE=CD=2,D是CE的中点,
∴OD=OE=CD=DE=2。
∴ 为等边三角形。
为等边三角形。
∴ 。
。
∵ ,
, ,
,
∴ ,∴
,∴ ,即
,即 。
。
根据勾股定理求得: ,
, 。
。
∴△ACE的周长为 。
。
(3)存在,这样的梯形有2个,(如图③所示),

连接OE,
由四边形AODE为梯形的定义可知:AE∥OD,
∴ 。
。
∵OD=CD,∴ 。
。
∴ ,∴AE=CE。
,∴AE=CE。
∵ ,
,
∴ ,
, 。
。
∴ ∽
∽ 。
。
∴ ,即:
,即: 。
。
∴ 。
。
(1)由已知,根据勾股定理的逆定理可得∠ODC=900,从而CD为⊙O的切线。
(2)由已知,判断△EOC和△EOA都是直角三角形,根据已知和勾股定理可求各边长而得到△ACE的周长。
(3)由梯形的定义可知:AE∥OD,根据平行线同位角相等的性质,和等腰三角形等边对等角的性质,可证得 ∽
∽ ,从而由比例式可求解。
,从而由比例式可求解。

练习册系列答案
相关题目
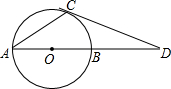 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=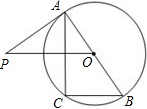 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.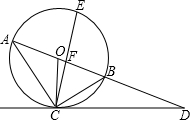

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,