题目内容
有一多边形草坪,在市政建设设计图纸上的面积为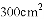 ,其中一条边的长度为
,其中一条边的长度为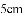
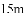
A. 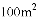 B.
B. 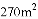 C.
C. 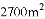 D.
D. 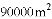
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
有一多边形草坪,在市政建设设计图纸上的面积为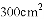 ,其中一条边的长度为
,其中一条边的长度为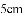
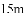
A. 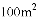 B.
B. 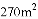 C.
C. 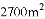 D.
D. 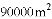
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案