��Ŀ����
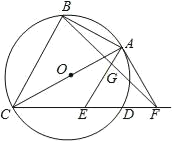
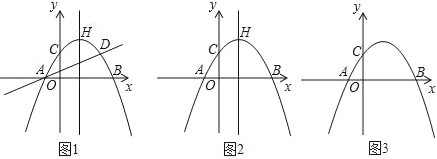
����Ŀ����ͼ��������y����![]() x2+bx+c��x�ύ��A����1��0����B��3��0������y�ύ��C�㣬��C���������ߵĶԳ���ĶԳƵ�Ϊ��D�������߶���ΪH��
x2+bx+c��x�ύ��A����1��0����B��3��0������y�ύ��C�㣬��C���������ߵĶԳ���ĶԳƵ�Ϊ��D�������߶���ΪH��
��1���������ߵĽ���ʽ��
��2������E�������ߵĶԳ������˶�ʱ����ֱ��AD���Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
��3����PΪֱ��AD�Ϸ������ߵĶԳ�����һ���㣬����PA��PD����S��PAD��3������x���ϴ����Զ���Q��ʹPQ+![]() QB��С�������ڣ���ֱ��д����ʱ��Q�����꼰PQ+
QB��С�������ڣ���ֱ��д����ʱ��Q�����꼰PQ+![]() QB����Сֵ��
QB����Сֵ��
���𰸡���1��![]() ��2����0��
��2����0��![]() ����2��
����2��![]() ����2����
����2����![]() ����3����2.5��0��
����3����2.5��0��
��������
��1����A����1��0����B��3��0�������뵽�����ߵĽ���ʽ�����ɽ��
��2�����ڣ�������������ۣ���EF����ACƽ�Ƶõ���C��EΪ��Ӧ�㣬A��FΪ��Ӧ�㣬�ٰ�F�����ֱ��AD�Ľ���ʽΪy��![]() x+
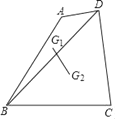
x+![]() �����ɽ�����ͼ2��ʾ����ʱ��F���D�غϣ����ɽ�����ͼ3��ʾ������ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
�����ɽ�����ͼ2��ʾ����ʱ��F���D�غϣ����ɽ�����ͼ3��ʾ������ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
�������ʽ���ɽ��
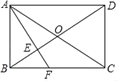
��3����ͼ4��ʾ������B��AD��ƽ���߽������ߵĶԳ����ڵ�N������P��PH��ֱ��BN����x��Ľ��㼴Ϊ��Q����ֱ��BN�Ľ���ʽΪy��![]() x+b������B��3��0�������BN�Ľ���ʽ�������ý���ʽ���M,N��ֵ�������PQ+
x+b������B��3��0�������BN�Ľ���ʽ�������ý���ʽ���M,N��ֵ�������PQ+![]() QB��PQ+QH����P��Q��H���㹲��ʱ��PQ+
QB��PQ+QH����P��Q��H���㹲��ʱ��PQ+![]() QB��С����ΪPH�����ɽ��
QB��С����ΪPH�����ɽ��
��1����������y����![]() x2+bx+c��x�ύ��A����1��0����B��3��0����
x2+bx+c��x�ύ��A����1��0����B��3��0����
��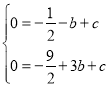 ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2�����ڣ�������������ۣ�
����ͼ1��ʾ��
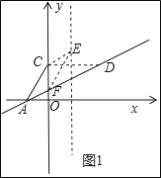
���ı���ACEFΪƽ���ı��Σ�
��EF����ACƽ�Ƶõ���C��EΪ��Ӧ�㣬A��FΪ��Ӧ�㣬
��C��0��![]() ������E�ĺ�����Ϊ1��
������E�ĺ�����Ϊ1��
������ƽ����һ����λ��
��A����1��0����
��F�ĺ�����Ϊ0��
��ֱ��AD�Ľ���ʽΪy��![]() x+
x+![]() ��
��
�൱x��0ʱ��y��![]() ��
��
��F��0��![]() ����
����
����ͼ2��ʾ��
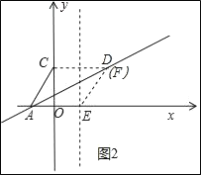
��ʱ��F���D�غϣ�
��F��2��![]() ����
����
����ͼ3��ʾ��
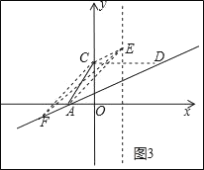
����ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
��x����2ʱ��y����![]() ��
��
��F����2����![]() ����
����
������������F��������0��![]() ����2��
����2��![]() ����2����
����2����![]() ����
����
��3����ͼ4��ʾ������B��AD��ƽ���߽������ߵĶԳ����ڵ�N������P��PH��ֱ��BN����x��Ľ��㼴Ϊ��Q��
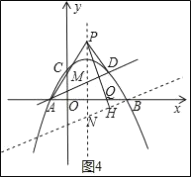
��ֱ��BN�Ľ���ʽΪy��![]() x+b������B��3��0����
x+b������B��3��0����
���b����![]() ��
��
��ֱ��BN�Ľ���ʽΪy��![]() x��
x��![]() ��
��
�������ߵĶԳ���Ϊֱ��x��1��
��N��1����1����
��ֱ��AD�������ߵĶԳ���Ľ���Ϊ��M��
��M��1��1����
��S��ADP��PM��xD��xA��![]() ��3��
��3��
��PM��2��
��P��1��3����
��tan��ABN��![]() ��
��
��![]() QB��QH��
QB��QH��
��PQ+![]() QB��PQ+QH��
QB��PQ+QH��
span>�൱P��Q��H���㹲��ʱ��PQ+![]() QB��С����ΪPH��
QB��С����ΪPH��
��PN��4����NPH����ABN��
��PH��![]() ��
��
��PQ+![]() QB����СֵΪ
QB����СֵΪ![]() ��
��
��ʱ��Q��2.5��0����

 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�