Question

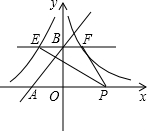（2013•保康县二模）若一次函数的图象与x轴、y轴分别交于点A（-2，0）、点B（0，2）．    
（1）求一次函数的解析式．
（2）若点C在x轴上，且OC=2

3

，请直接写出∠ABC的度数．
（3）若直线EF经过点B且平行于X轴，交反比例函数y=-

4

x

于点E，交反比例函数y=

2

x

于点F，点P是x轴上一动点，请直接写出△PEF的面积．

Answer 1

分析：（1）用待定系数法将A，B两点代入，得出一次函数的解析式即可．
（2）点C有两种位置，在正半轴或负半轴，正半轴时∠ABC=105°，C在负半轴上时∠ABC=15°；
（3）根据E，F点纵坐标得出横坐标，进而得出EF的长，再利用三角形面积公式求出s_△PEF=3．

解答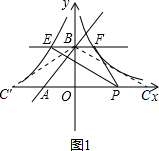：解：（1）∵一次函数的图象与x轴、y轴分别交于点A（-2，0）、点B（0，2），
∴设一次函数解析式为y=kx+b，则

b=2 -2k+b=0

，
解得：

k=1 b=2

∴一次函数的解析式为：y=x+2；
                         
（2）当点C在正半轴时，∵A（-2，0）、点B（0，2），
∴AO=BO=2，
∴∠ABO=45°，
∵BO=2，CO=2

3

，
∴tan∠CBO=

2 3

2

=

3

，
∴∠CBO=60°，
∴∠ABC=60°+45°=105°，
同理可得出：C在负半轴上时，∠ABC′=60°-45°=15°；
综上所述：在正半轴或负半轴，正半轴时∠ABC=105°，C在负半轴上时∠ABC=15°；
          
（3）∵直线EF经过点B且平行于X轴，交反比例函数y=-

4

x

于点E，交反比例函数y=

2

x

于点F，
∴E点横坐标为：3=-

4

x

，则x=-

4

3

，
F点横坐标为：3=

2

x

，则x=

2

3

，
∴EF=

2

3

-（

4

3

）=2，
s_△PEF=

1

2

×2×3=3．

点评：此题主要考查了反比例函数图象上点的性质以及三角形面积求法和待定系数法求一次函数解析式以及锐角三角函数的应用等知识，利用分类讨论的思想以及数形结合得出是解题关键．